Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 33096 by 7991 last updated on 10/Apr/18

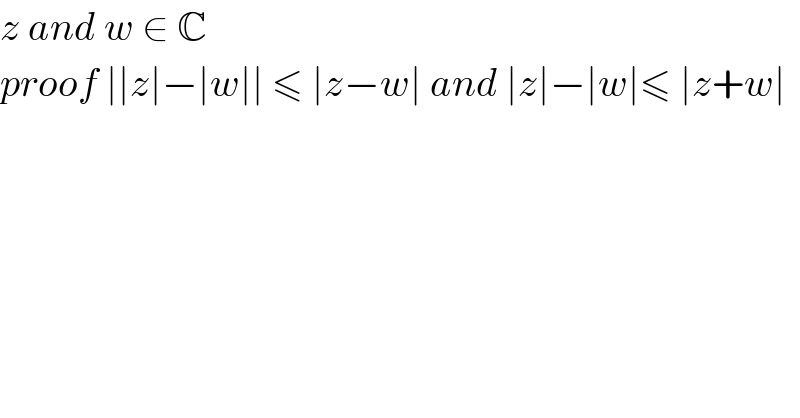
z and w ∈ C proof ∣∣z∣−∣w∣∣ ≤ ∣z−w∣ and ∣z∣−∣w∣≤ ∣z+w∣

$${z}\:{and}\:{w}\:\in\:\mathbb{C} \\ $$$${proof}\:\mid\mid{z}\mid−\mid{w}\mid\mid\:\leqslant\:\mid{z}−{w}\mid\:{and}\:\mid{z}\mid−\mid{w}\mid\leqslant\:\mid{z}+{w}\mid \\ $$

Answered by MJS last updated on 10/Apr/18

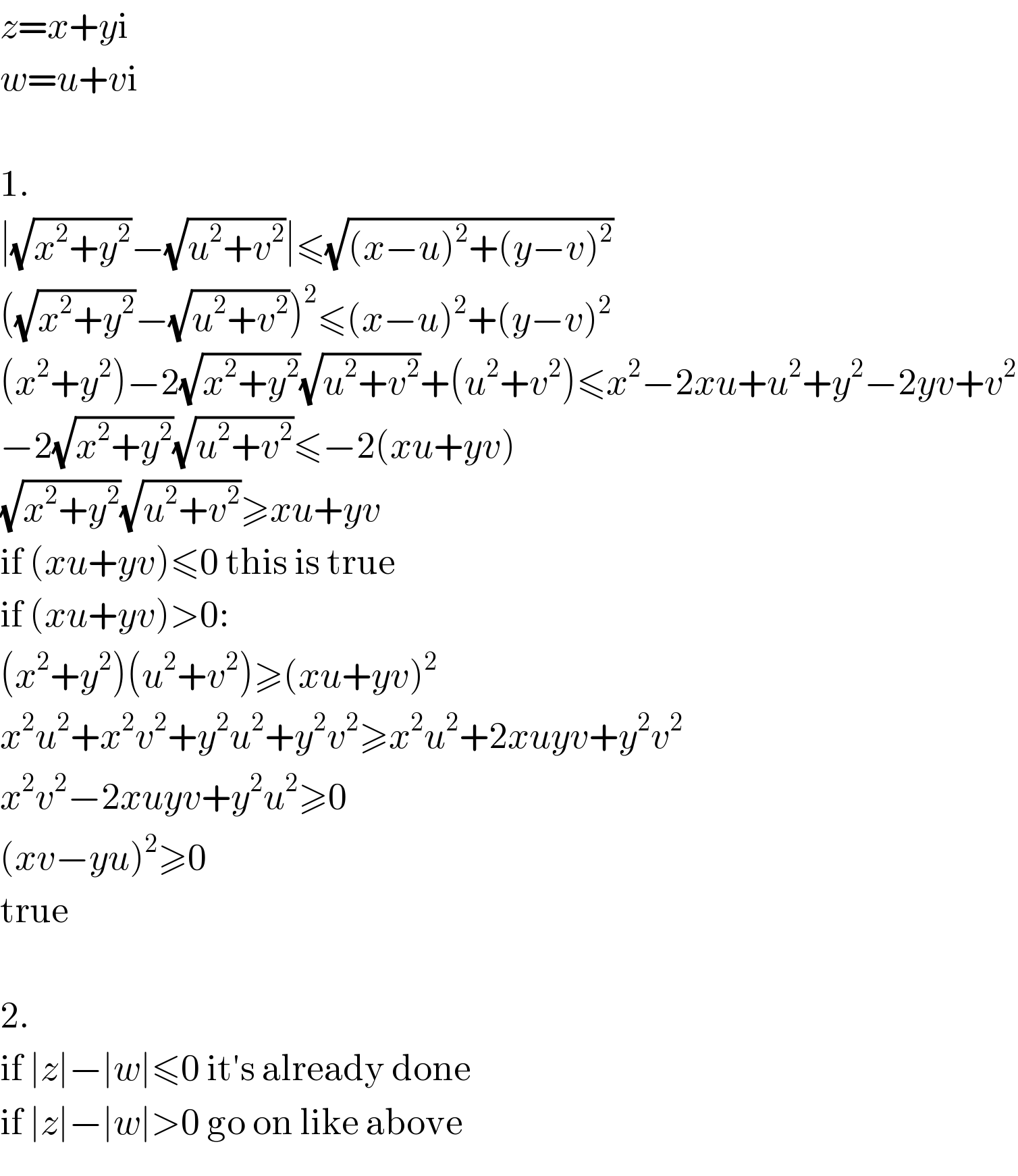
z=x+yi w=u+vi 1. ∣(√(x^2 +y^2 ))−(√(u^2 +v^2 ))∣≤(√((x−u)^2 +(y−v)^2 )) ((√(x^2 +y^2 ))−(√(u^2 +v^2 )))^2 ≤(x−u)^2 +(y−v)^2 (x^2 +y^2 )−2(√(x^2 +y^2 ))(√(u^2 +v^2 ))+(u^2 +v^2 )≤x^2 −2xu+u^2 +y^2 −2yv+v^2 −2(√(x^2 +y^2 ))(√(u^2 +v^2 ))≤−2(xu+yv) (√(x^2 +y^2 ))(√(u^2 +v^2 ))≥xu+yv if (xu+yv)≤0 this is true if (xu+yv)>0: (x^2 +y^2 )(u^2 +v^2 )≥(xu+yv)^2 x^2 u^2 +x^2 v^2 +y^2 u^2 +y^2 v^2 ≥x^2 u^2 +2xuyv+y^2 v^2 x^2 v^2 −2xuyv+y^2 u^2 ≥0 (xv−yu)^2 ≥0 true 2. if ∣z∣−∣w∣≤0 it′s already done if ∣z∣−∣w∣>0 go on like above

$${z}={x}+{y}\mathrm{i} \\ $$$${w}={u}+{v}\mathrm{i} \\ $$$$ \\ $$$$\mathrm{1}. \\ $$$$\mid\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }\mid\leqslant\sqrt{\left({x}−{u}\right)^{\mathrm{2}} +\left({y}−{v}\right)^{\mathrm{2}} } \\ $$$$\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }−\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }\right)^{\mathrm{2}} \leqslant\left({x}−{u}\right)^{\mathrm{2}} +\left({y}−{v}\right)^{\mathrm{2}} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }+\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\leqslant{x}^{\mathrm{2}} −\mathrm{2}{xu}+{u}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{yv}+{v}^{\mathrm{2}} \\ $$$$−\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }\leqslant−\mathrm{2}\left({xu}+{yv}\right) \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }\geqslant{xu}+{yv} \\ $$$$\mathrm{if}\:\left({xu}+{yv}\right)\leqslant\mathrm{0}\:\mathrm{this}\:\mathrm{is}\:\mathrm{true} \\ $$$$\mathrm{if}\:\left({xu}+{yv}\right)>\mathrm{0}: \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\geqslant\left({xu}+{yv}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {u}^{\mathrm{2}} +{x}^{\mathrm{2}} {v}^{\mathrm{2}} +{y}^{\mathrm{2}} {u}^{\mathrm{2}} +{y}^{\mathrm{2}} {v}^{\mathrm{2}} \geqslant{x}^{\mathrm{2}} {u}^{\mathrm{2}} +\mathrm{2}{xuyv}+{y}^{\mathrm{2}} {v}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {v}^{\mathrm{2}} −\mathrm{2}{xuyv}+{y}^{\mathrm{2}} {u}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\left({xv}−{yu}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{true} \\ $$$$ \\ $$$$\mathrm{2}. \\ $$$$\mathrm{if}\:\mid{z}\mid−\mid{w}\mid\leqslant\mathrm{0}\:\mathrm{it}'\mathrm{s}\:\mathrm{already}\:\mathrm{done} \\ $$$$\mathrm{if}\:\mid{z}\mid−\mid{w}\mid>\mathrm{0}\:\mathrm{go}\:\mathrm{on}\:\mathrm{like}\:\mathrm{above} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com