
Question Number 140709 by mathdanisur last updated on 11/May/21

$$\frac{{z}^{\mathrm{999}} −\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)\centerdot\left({z}^{\mathrm{2}} +{z}+\mathrm{1}\right)} \\ $$$${find}\:{the}\:{sum}\:{of}\:{the}\:{coefficientes}\:{of} \\ $$$${the}\:{polynomial}\:{obtained}\:{bh}\:{dividing} \\ $$$${the}\:{expression}\:{by}\:{the}\:{polynomial}... \\ $$
Commented by mr W last updated on 11/May/21

$${sum}=\mathrm{0} \\ $$
Commented by mathdanisur last updated on 11/May/21
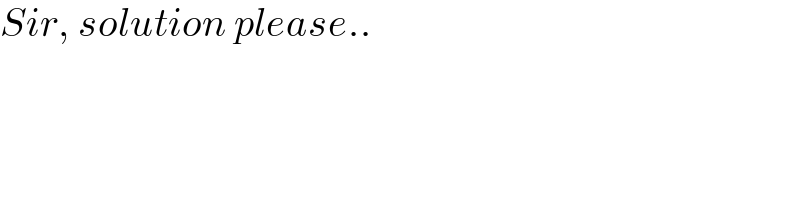
$${Sir},\:{solution}\:{please}.. \\ $$
Commented by mr W last updated on 11/May/21
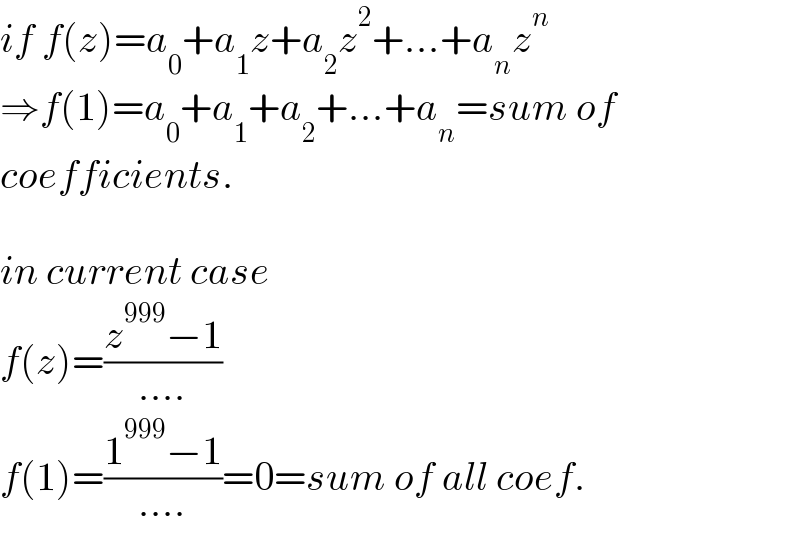
$${if}\:{f}\left({z}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {z}+{a}_{\mathrm{2}} {z}^{\mathrm{2}} +...+{a}_{{n}} {z}^{{n}} \\ $$$$\Rightarrow{f}\left(\mathrm{1}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +...+{a}_{{n}} ={sum}\:{of} \\ $$$${coefficients}. \\ $$$$ \\ $$$${in}\:{current}\:{case}\: \\ $$$${f}\left({z}\right)=\frac{{z}^{\mathrm{999}} −\mathrm{1}}{....} \\ $$$${f}\left(\mathrm{1}\right)=\frac{\mathrm{1}^{\mathrm{999}} −\mathrm{1}}{....}=\mathrm{0}={sum}\:{of}\:{all}\:{coef}. \\ $$
Commented by mathdanisur last updated on 12/May/21

$${cool}\:{Sir}\:{thak}\:{you} \\ $$
