Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145344 by mathdanisur last updated on 04/Jul/21

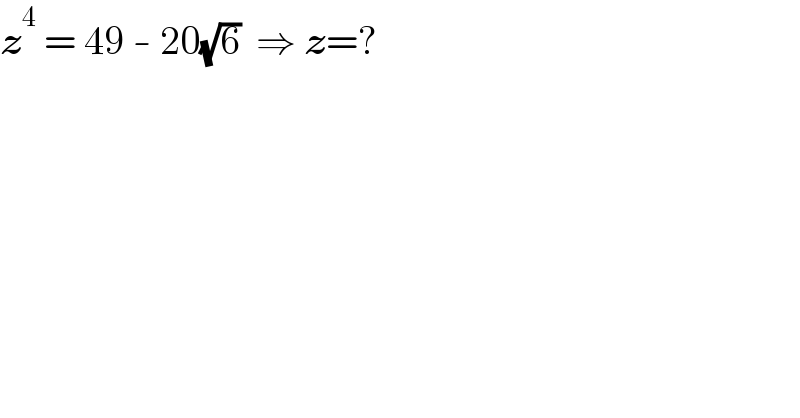
z^4 = 49 - 20(√6) ⇒ z=?

$$\boldsymbol{{z}}^{\mathrm{4}} \:=\:\mathrm{49}\:-\:\mathrm{20}\sqrt{\mathrm{6}}\:\:\Rightarrow\:\boldsymbol{{z}}=? \\ $$

Answered by liberty last updated on 04/Jul/21

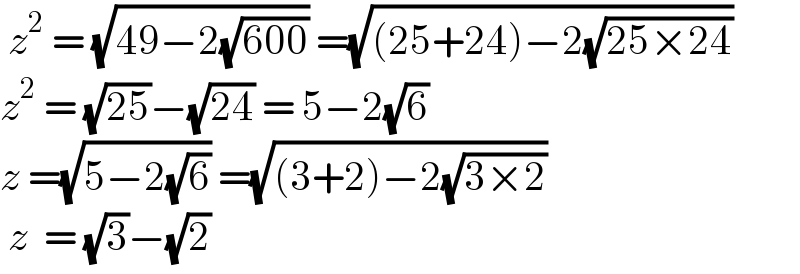
z^2 = (√(49−2(√(600)))) =(√((25+24)−2(√(25×24)))) z^2 = (√(25))−(√(24)) = 5−2(√6) z =(√(5−2(√6))) =(√((3+2)−2(√(3×2)))) z = (√3)−(√2)

$$\:{z}^{\mathrm{2}} \:=\:\sqrt{\mathrm{49}−\mathrm{2}\sqrt{\mathrm{600}}}\:=\sqrt{\left(\mathrm{25}+\mathrm{24}\right)−\mathrm{2}\sqrt{\mathrm{25}×\mathrm{24}}} \\ $$$${z}^{\mathrm{2}} \:=\:\sqrt{\mathrm{25}}−\sqrt{\mathrm{24}}\:=\:\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\: \\ $$$${z}\:=\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}}\:=\sqrt{\left(\mathrm{3}+\mathrm{2}\right)−\mathrm{2}\sqrt{\mathrm{3}×\mathrm{2}}} \\ $$$$\:{z}\:\:=\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\: \\ $$

Commented by mathdanisur last updated on 04/Jul/21

thank you Ser

$${thank}\:{you}\:{Ser} \\ $$

Answered by Olaf_Thorendsen last updated on 04/Jul/21

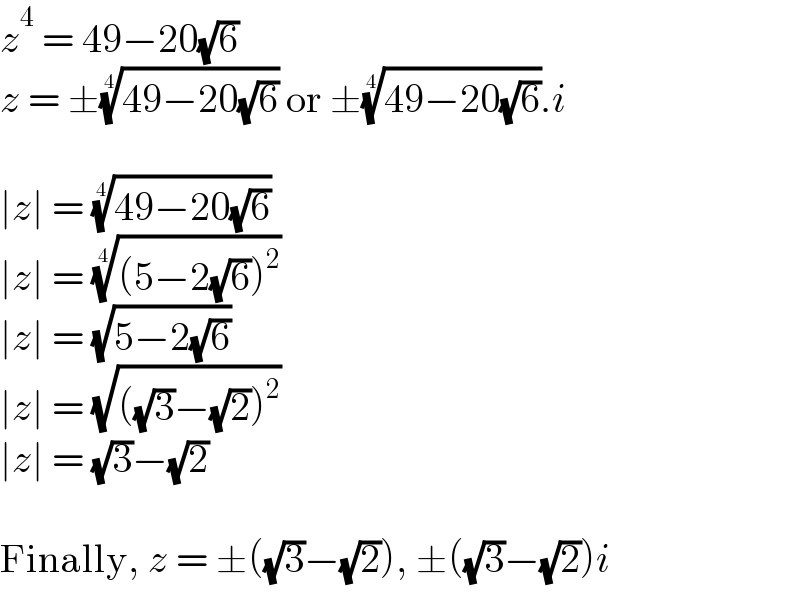
z^4 = 49−20(√6) z = ±((49−20(√6)))^(1/4) or ±((49−20(√6)))^(1/4) .i ∣z∣ = ((49−20(√6)))^(1/4) ∣z∣ = (((5−2(√6))^2 ))^(1/4) ∣z∣ = (√(5−2(√6))) ∣z∣ = (√(((√3)−(√2))^2 )) ∣z∣ = (√3)−(√2) Finally, z = ±((√3)−(√2)), ±((√3)−(√2))i

$${z}^{\mathrm{4}} \:=\:\mathrm{49}−\mathrm{20}\sqrt{\mathrm{6}} \\ $$$${z}\:=\:\pm\sqrt[{\mathrm{4}}]{\mathrm{49}−\mathrm{20}\sqrt{\mathrm{6}}}\:\mathrm{or}\:\pm\sqrt[{\mathrm{4}}]{\mathrm{49}−\mathrm{20}\sqrt{\mathrm{6}}}.{i} \\ $$$$ \\ $$$$\mid{z}\mid\:=\:\sqrt[{\mathrm{4}}]{\mathrm{49}−\mathrm{20}\sqrt{\mathrm{6}}} \\ $$$$\mid{z}\mid\:=\:\sqrt[{\mathrm{4}}]{\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{2}} } \\ $$$$\mid{z}\mid\:=\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$\mid{z}\mid\:=\:\sqrt{\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mid{z}\mid\:=\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Finally},\:{z}\:=\:\pm\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right),\:\pm\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right){i} \\ $$

Commented by mathdanisur last updated on 04/Jul/21

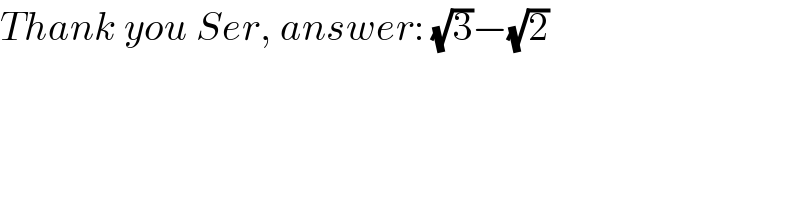
Thank you Ser, answer: (√3)−(√2)

$${Thank}\:{you}\:{Ser},\:{answer}:\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$

Commented by mr W last updated on 04/Jul/21

if (√3)−(√2) is a root, then −((√3)−(√2)) is also a root, and ((√3)−(√2))i is also a root, and −((√3)−(√2))i is also a root.

$${if}\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\:{is}\:{a}\:{root},\:{then} \\ $$$$−\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)\:{is}\:{also}\:{a}\:{root},\:{and} \\ $$$$\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right){i}\:{is}\:{also}\:{a}\:{root},\:{and} \\ $$$$−\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right){i}\:{is}\:{also}\:{a}\:{root}. \\ $$

Commented by mathdanisur last updated on 04/Jul/21

Thanks Sir

$${Thanks}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com