Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 142582 by mathdanisur last updated on 02/Jun/21

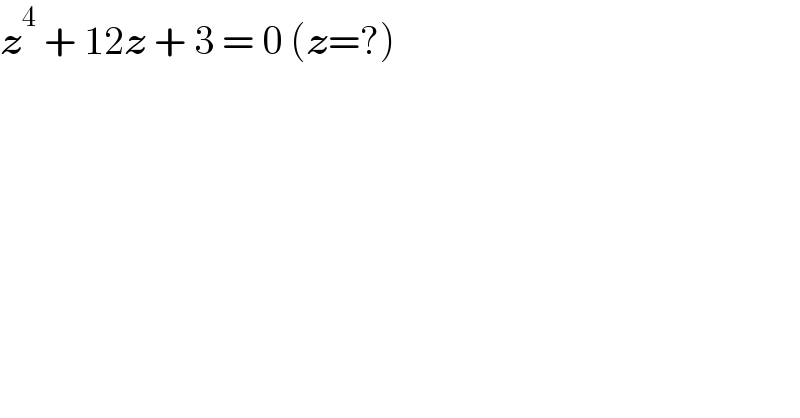
z^4 + 12z + 3 = 0 (z=?)

$$\boldsymbol{{z}}^{\mathrm{4}} \:+\:\mathrm{12}\boldsymbol{{z}}\:+\:\mathrm{3}\:=\:\mathrm{0}\:\left(\boldsymbol{{z}}=?\right) \\ $$

Answered by ajfour last updated on 02/Jun/21

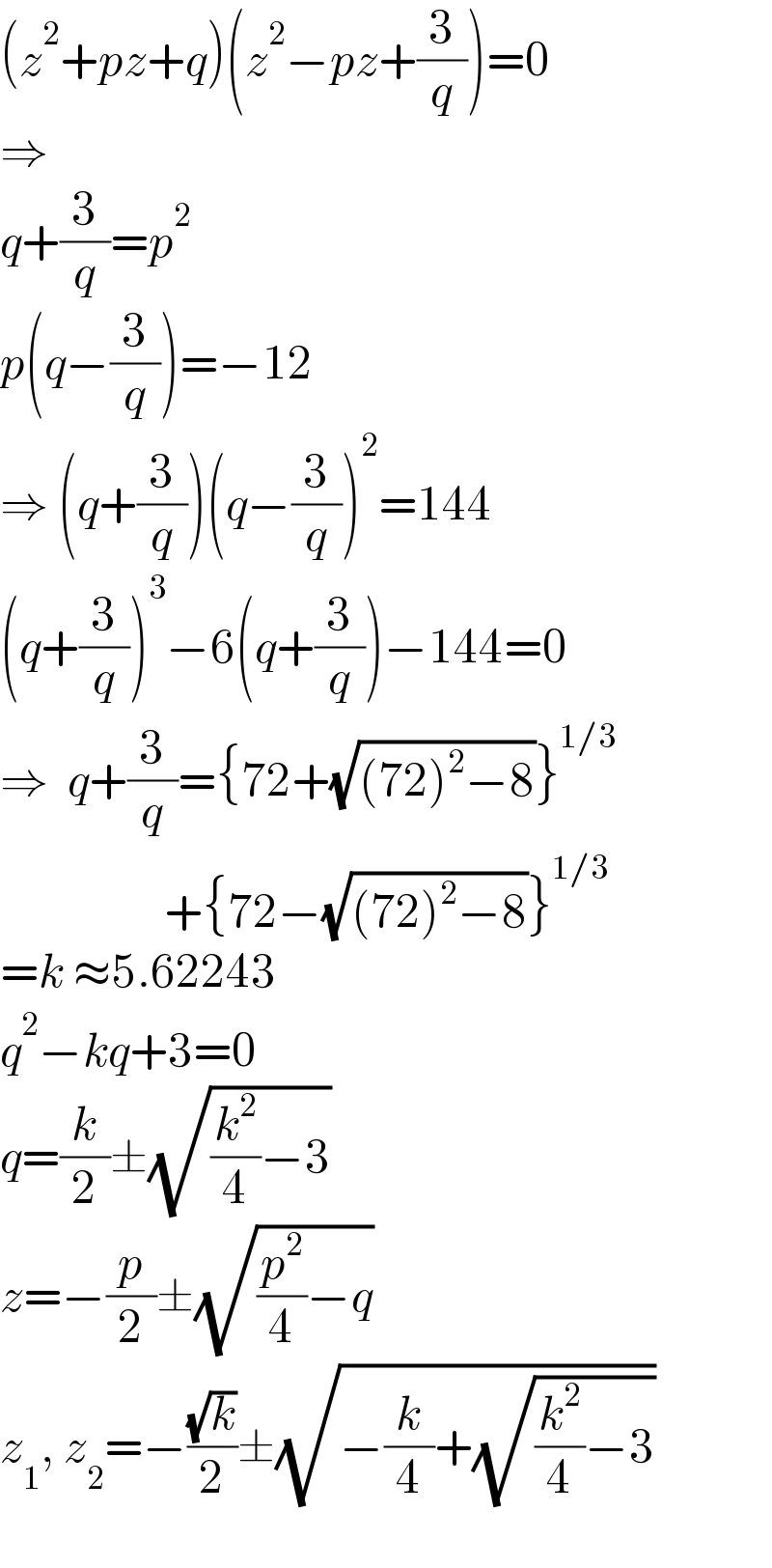
(z^2 +pz+q)(z^2 −pz+(3/q))=0 ⇒ q+(3/q)=p^2 p(q−(3/q))=−12 ⇒ (q+(3/q))(q−(3/q))^2 =144 (q+(3/q))^3 −6(q+(3/q))−144=0 ⇒ q+(3/q)={72+(√((72)^2 −8))}^(1/3) +{72−(√((72)^2 −8))}^(1/3) =k ≈5.62243 q^2 −kq+3=0 q=(k/2)±(√((k^2 /4)−3)) z=−(p/2)±(√((p^2 /4)−q)) z_1 , z_2 =−((√k)/2)±(√(−(k/4)+(√((k^2 /4)−3))))

$$\left({z}^{\mathrm{2}} +{pz}+{q}\right)\left({z}^{\mathrm{2}} −{pz}+\frac{\mathrm{3}}{{q}}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${q}+\frac{\mathrm{3}}{{q}}={p}^{\mathrm{2}} \\ $$$${p}\left({q}−\frac{\mathrm{3}}{{q}}\right)=−\mathrm{12} \\ $$$$\Rightarrow\:\left({q}+\frac{\mathrm{3}}{{q}}\right)\left({q}−\frac{\mathrm{3}}{{q}}\right)^{\mathrm{2}} =\mathrm{144} \\ $$$$\left({q}+\frac{\mathrm{3}}{{q}}\right)^{\mathrm{3}} −\mathrm{6}\left({q}+\frac{\mathrm{3}}{{q}}\right)−\mathrm{144}=\mathrm{0} \\ $$$$\Rightarrow\:\:{q}+\frac{\mathrm{3}}{{q}}=\left\{\mathrm{72}+\sqrt{\left(\mathrm{72}\right)^{\mathrm{2}} −\mathrm{8}}\right\}^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left\{\mathrm{72}−\sqrt{\left(\mathrm{72}\right)^{\mathrm{2}} −\mathrm{8}}\right\}^{\mathrm{1}/\mathrm{3}} \\ $$$$={k}\:\approx\mathrm{5}.\mathrm{62243} \\ $$$${q}^{\mathrm{2}} −{kq}+\mathrm{3}=\mathrm{0} \\ $$$${q}=\frac{{k}}{\mathrm{2}}\pm\sqrt{\frac{{k}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{3}} \\ $$$${z}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$${z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} =−\frac{\sqrt{{k}}}{\mathrm{2}}\pm\sqrt{−\frac{{k}}{\mathrm{4}}+\sqrt{\frac{{k}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{3}}} \\ $$$$ \\ $$

Answered by MJS_new last updated on 02/Jun/21

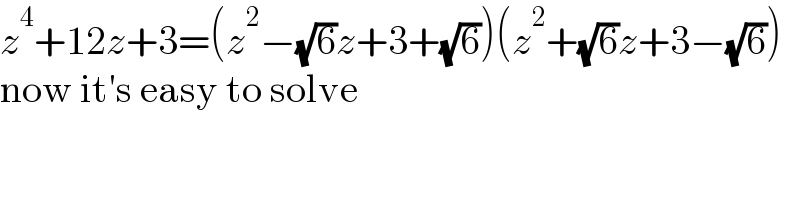
z^4 +12z+3=(z^2 −(√6)z+3+(√6))(z^2 +(√6)z+3−(√6)) now it′s easy to solve

$${z}^{\mathrm{4}} +\mathrm{12}{z}+\mathrm{3}=\left({z}^{\mathrm{2}} −\sqrt{\mathrm{6}}{z}+\mathrm{3}+\sqrt{\mathrm{6}}\right)\left({z}^{\mathrm{2}} +\sqrt{\mathrm{6}}{z}+\mathrm{3}−\sqrt{\mathrm{6}}\right) \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$

Commented by MJS_new last updated on 02/Jun/21

you′re welcome!

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome}! \\ $$

Commented by mr W last updated on 02/Jun/21

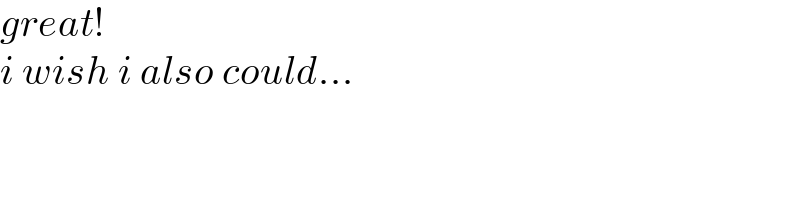
great! i wish i also could...

$${great}! \\ $$$${i}\:{wish}\:{i}\:{also}\:{could}... \\ $$

Commented by MJS_new last updated on 02/Jun/21

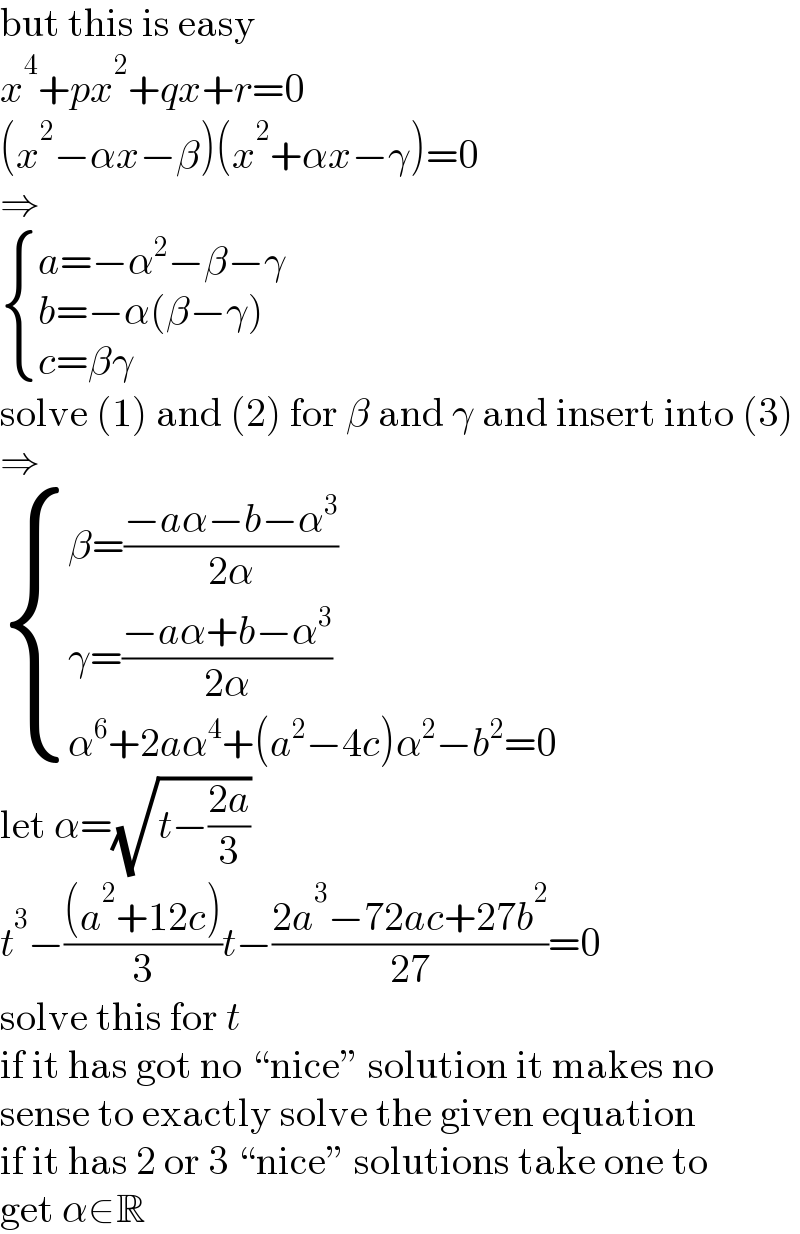
but this is easy x^4 +px^2 +qx+r=0 (x^2 −αx−β)(x^2 +αx−γ)=0 ⇒ { ((a=−α^2 −β−γ)),((b=−α(β−γ))),((c=βγ)) :} solve (1) and (2) for β and γ and insert into (3) ⇒ { ((β=((−aα−b−α^3 )/(2α)))),((γ=((−aα+b−α^3 )/(2α)))),((α^6 +2aα^4 +(a^2 −4c)α^2 −b^2 =0)) :} let α=(√(t−((2a)/3))) t^3 −(((a^2 +12c))/3)t−((2a^3 −72ac+27b^2 )/(27))=0 solve this for t if it has got no “nice” solution it makes no sense to exactly solve the given equation if it has 2 or 3 “nice” solutions take one to get α∈R

$$\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{easy} \\ $$$${x}^{\mathrm{4}} +{px}^{\mathrm{2}} +{qx}+{r}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\alpha{x}−\beta\right)\left({x}^{\mathrm{2}} +\alpha{x}−\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{a}=−\alpha^{\mathrm{2}} −\beta−\gamma}\\{{b}=−\alpha\left(\beta−\gamma\right)}\\{{c}=\beta\gamma}\end{cases} \\ $$$$\mathrm{solve}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{for}\:\beta\:\mathrm{and}\:\gamma\:\mathrm{and}\:\mathrm{insert}\:\mathrm{into}\:\left(\mathrm{3}\right) \\ $$$$\Rightarrow \\ $$$$\begin{cases}{\beta=\frac{−{a}\alpha−{b}−\alpha^{\mathrm{3}} }{\mathrm{2}\alpha}}\\{\gamma=\frac{−{a}\alpha+{b}−\alpha^{\mathrm{3}} }{\mathrm{2}\alpha}}\\{\alpha^{\mathrm{6}} +\mathrm{2}{a}\alpha^{\mathrm{4}} +\left({a}^{\mathrm{2}} −\mathrm{4}{c}\right)\alpha^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0}}\end{cases} \\ $$$$\mathrm{let}\:\alpha=\sqrt{{t}−\frac{\mathrm{2}{a}}{\mathrm{3}}} \\ $$$${t}^{\mathrm{3}} −\frac{\left({a}^{\mathrm{2}} +\mathrm{12}{c}\right)}{\mathrm{3}}{t}−\frac{\mathrm{2}{a}^{\mathrm{3}} −\mathrm{72}{ac}+\mathrm{27}{b}^{\mathrm{2}} }{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{t} \\ $$$$\mathrm{if}\:\mathrm{it}\:\mathrm{has}\:\mathrm{got}\:\mathrm{no}\:``\mathrm{nice}''\:\mathrm{solution}\:\mathrm{it}\:\mathrm{makes}\:\mathrm{no} \\ $$$$\mathrm{sense}\:\mathrm{to}\:\mathrm{exactly}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{if}\:\mathrm{it}\:\mathrm{has}\:\mathrm{2}\:\mathrm{or}\:\mathrm{3}\:``\mathrm{nice}''\:\mathrm{solutions}\:\mathrm{take}\:\mathrm{one}\:\mathrm{to} \\ $$$$\mathrm{get}\:\alpha\in\mathbb{R} \\ $$

Commented by mr W last updated on 02/Jun/21

thanks sir!

$${thanks}\:{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com