
Question Number 7021 by FilupSmith last updated on 06/Aug/16

$${z}=\int_{\mathrm{0}} ^{\:{t}} {i}\left(−\mathrm{1}\right)^{{x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\:{t}} {ie}^{{i}\pi{x}} {dx} \\ $$$$ \\ $$$$\left(\mathrm{1}\right) \\ $$$$={i}\int_{\mathrm{0}} ^{\:{t}} {e}^{{i}\pi{x}} {dx} \\ $$$$={i}\left(\frac{\mathrm{1}}{{i}\pi}\left({e}^{{i}\pi{t}} −\mathrm{1}\right)\right) \\ $$$${z}=\frac{\mathrm{1}}{\pi}\left(\left(−\mathrm{1}\right)^{{t}} −\mathrm{1}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$=\int_{\mathrm{0}} ^{\:{t}} {ie}^{{i}\pi{x}} {dx} \\ $$$${u}={e}^{{i}\pi{x}} \:\Rightarrow\:{du}=\frac{\mathrm{1}}{{i}\pi}{e}^{{i}\pi{x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\:{t}} \frac{{i}\pi}{{i}\pi}{ie}^{{i}\pi{x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\:{t}} {i}\pi{idu} \\ $$$$=−\pi\int_{\mathrm{0}} ^{\:{t}} {du} \\ $$$$=−\pi\left({e}^{{i}\pi{t}} −\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{incorrect}? \\ $$
Commented by FilupSmith last updated on 07/Aug/16
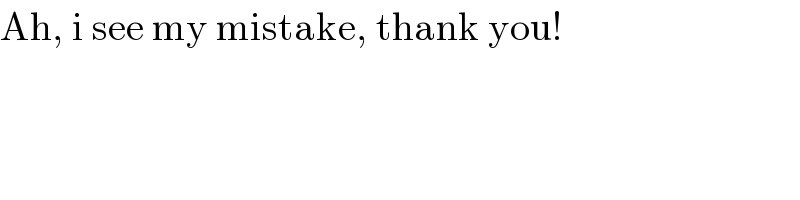
$$\mathrm{Ah},\:\mathrm{i}\:\mathrm{see}\:\mathrm{my}\:\mathrm{mistake},\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by Yozzii last updated on 06/Aug/16
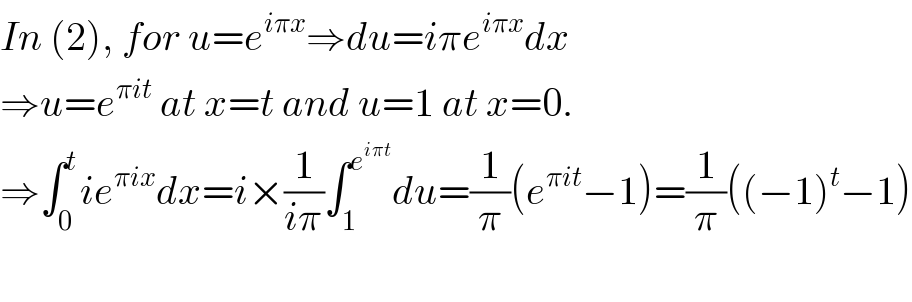
$${In}\:\left(\mathrm{2}\right),\:{for}\:{u}={e}^{{i}\pi{x}} \Rightarrow{du}={i}\pi{e}^{{i}\pi{x}} {dx} \\ $$$$\Rightarrow{u}={e}^{\pi{it}} \:{at}\:{x}={t}\:{and}\:{u}=\mathrm{1}\:{at}\:{x}=\mathrm{0}. \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{{t}} {ie}^{\pi{ix}} {dx}={i}×\frac{\mathrm{1}}{{i}\pi}\int_{\mathrm{1}} ^{{e}^{{i}\pi{t}} } {du}=\frac{\mathrm{1}}{\pi}\left({e}^{\pi{it}} −\mathrm{1}\right)=\frac{\mathrm{1}}{\pi}\left(\left(−\mathrm{1}\right)^{{t}} −\mathrm{1}\right) \\ $$$$ \\ $$
Answered by Yozzii last updated on 08/Aug/16
$${Check}\:{for}\:{a}\:{response}\:{in}\:{the}\:{comments}. \\ $$
