Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 188551 by mr W last updated on 03/Mar/23

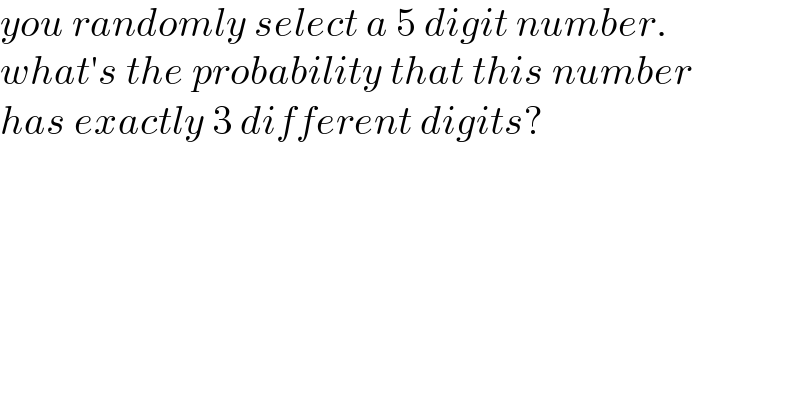
you randomly select a 5 digit number. what′s the probability that this number has exactly 3 different digits?

$${you}\:{randomly}\:{select}\:{a}\:\mathrm{5}\:{digit}\:{number}. \\ $$$${what}'{s}\:{the}\:{probability}\:{that}\:{this}\:{number} \\ $$$${has}\:{exactly}\:\mathrm{3}\:{different}\:{digits}? \\ $$

Answered by mr W last updated on 03/Mar/23

from 10000 to 99999 there are totally 90000 5 digit numbers. now we want to find how many among them have exactly 3 digits. to select 3 digits from 0 to 9 there are C_3 ^(10) possibilities. say a, b, c are the digits we have selected. to form a 5 digit number using them we have following possibilities: 1) aaabc ⇒C_1 ^3 ×((5!)/(3!))=60 numbers 2) aabbc ⇒C_1 ^3 ×((5!)/(2!2!))=90 numbers in sum we have 150 numbers using a,b,c ⇒150×C_3 ^(10) =18000 numbers but among them some begin with the digit 0 like 0abab. to select a, b from 1 to 9 there are C_2 ^9 possibilities. 1) 0aaab ⇒2×((4!)/(3!))=8 numbers 2) 0aabb ⇒((4!)/(2!2!))=6 numbers 3) 000ab ⇒((4!)/(2!))=12 numbers 4) 00aab ⇒2×((4!)/(2!))=24 numbers in sum there are (8+6+12+24)×C_2 ^9 =1800 numbers which begin with 0. so we have 18000−1800=16200 numbers with exactly 3 digits. probability p=((16200)/(90000))=18% ✓

$${from}\:\mathrm{10000}\:{to}\:\mathrm{99999}\:{there}\:{are}\:{totally} \\ $$$$\mathrm{90000}\:\mathrm{5}\:{digit}\:{numbers}. \\ $$$${now}\:{we}\:{want}\:{to}\:{find}\:{how}\:{many}\:{among} \\ $$$${them}\:{have}\:{exactly}\:\mathrm{3}\:{digits}. \\ $$$${to}\:{select}\:\mathrm{3}\:{digits}\:{from}\:\mathrm{0}\:{to}\:\mathrm{9}\:{there}\:{are} \\ $$$${C}_{\mathrm{3}} ^{\mathrm{10}} \:{possibilities}.\:{say}\:{a},\:{b},\:{c}\:{are}\:{the} \\ $$$${digits}\:{we}\:{have}\:{selected}.\:{to}\:{form}\:{a}\:\mathrm{5} \\ $$$${digit}\:{number}\:{using}\:{them}\:{we}\:{have} \\ $$$${following}\:{possibilities}: \\ $$$$\left.\mathrm{1}\right)\:{aaabc} \\ $$$$\Rightarrow{C}_{\mathrm{1}} ^{\mathrm{3}} ×\frac{\mathrm{5}!}{\mathrm{3}!}=\mathrm{60}\:{numbers} \\ $$$$\left.\mathrm{2}\right)\:{aabbc} \\ $$$$\Rightarrow{C}_{\mathrm{1}} ^{\mathrm{3}} ×\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{90}\:{numbers} \\ $$$${in}\:{sum}\:{we}\:{have}\:\mathrm{150}\:{numbers}\:{using} \\ $$$${a},{b},{c} \\ $$$$\Rightarrow\mathrm{150}×{C}_{\mathrm{3}} ^{\mathrm{10}} =\mathrm{18000}\:{numbers} \\ $$$${but}\:{among}\:{them}\:{some}\:{begin}\:{with}\:{the} \\ $$$${digit}\:\mathrm{0}\:{like}\:\mathrm{0}{abab}. \\ $$$${to}\:{select}\:{a},\:{b}\:{from}\:\mathrm{1}\:{to}\:\mathrm{9}\:{there}\:{are} \\ $$$${C}_{\mathrm{2}} ^{\mathrm{9}} \:{possibilities}. \\ $$$$\left.\mathrm{1}\right)\:\mathrm{0}{aaab} \\ $$$$\Rightarrow\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{3}!}=\mathrm{8}\:{numbers} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{0}{aabb} \\ $$$$\Rightarrow\frac{\mathrm{4}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{6}\:{numbers} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{000}{ab} \\ $$$$\Rightarrow\frac{\mathrm{4}!}{\mathrm{2}!}=\mathrm{12}\:{numbers} \\ $$$$\left.\mathrm{4}\right)\:\mathrm{00}{aab} \\ $$$$\Rightarrow\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{2}!}=\mathrm{24}\:{numbers} \\ $$$${in}\:{sum}\:{there}\:{are}\: \\ $$$$\left(\mathrm{8}+\mathrm{6}+\mathrm{12}+\mathrm{24}\right)×{C}_{\mathrm{2}} ^{\mathrm{9}} =\mathrm{1800}\:{numbers} \\ $$$${which}\:{begin}\:{with}\:\mathrm{0}. \\ $$$${so}\:{we}\:{have}\:\mathrm{18000}−\mathrm{1800}=\mathrm{16200}\: \\ $$$${numbers}\:{with}\:{exactly}\:\mathrm{3}\:{digits}. \\ $$$${probability}\:{p}=\frac{\mathrm{16200}}{\mathrm{90000}}=\mathrm{18\%}\:\checkmark \\ $$

Commented by mr W last updated on 03/Mar/23

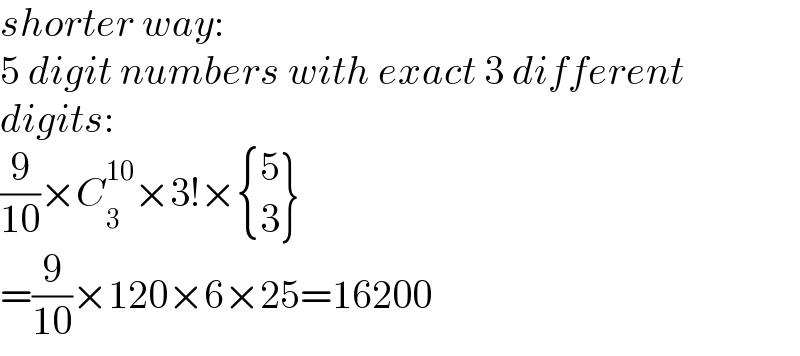
shorter way: 5 digit numbers with exact 3 different digits: (9/(10))×C_3 ^(10) ×3!× { (5),(3) :}} =(9/(10))×120×6×25=16200

$${shorter}\:{way}: \\ $$$$\mathrm{5}\:{digit}\:{numbers}\:{with}\:{exact}\:\mathrm{3}\:{different} \\ $$$${digits}: \\ $$$$\left.\frac{\mathrm{9}}{\mathrm{10}}×{C}_{\mathrm{3}} ^{\mathrm{10}} ×\mathrm{3}!×\begin{cases}{\mathrm{5}}\\{\mathrm{3}}\end{cases}\right\} \\ $$$$=\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{120}×\mathrm{6}×\mathrm{25}=\mathrm{16200} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com