
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 113710 by mr W last updated on 14/Sep/20

$${you}\:{have}\:\mathrm{2}\:{identical}\:{mathematics} \\ $$$${books},\:\mathrm{2}\:{identical}\:{physics}\:{books},\:\mathrm{2} \\ $$$${identical}\:{chemistry}\:{books},\:\mathrm{2}\:{identical} \\ $$$${biology}\:{books}\:{and}\:\mathrm{2}\:{geography}\:{books}. \\ $$$${in}\:{how}\:{many}\:{ways}\:{can}\:{you}\:{compile} \\ $$$${these}\:{books}\:{such}\:{that}\:{same}\:{books} \\ $$$${are}\:{not}\:{mutually}\:{adjacent}? \\ $$
Commented by I want to learn more last updated on 16/Sep/20
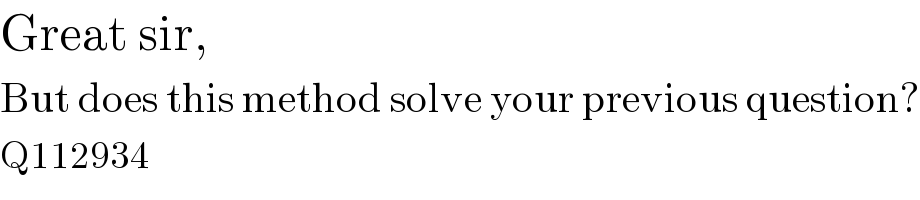
$$\mathrm{Great}\:\mathrm{sir}, \\ $$$$\mathrm{But}\:\mathrm{does}\:\mathrm{this}\:\mathrm{method}\:\mathrm{solve}\:\mathrm{your}\:\mathrm{previous}\:\mathrm{question}? \\ $$$$\mathrm{Q112934} \\ $$
Commented by mr W last updated on 16/Sep/20

$${no} \\ $$
Answered by mr W last updated on 15/Sep/20
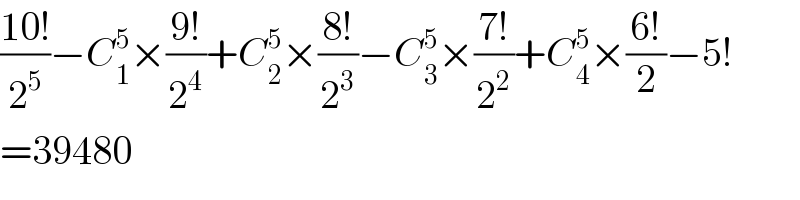
$$\frac{\mathrm{10}!}{\mathrm{2}^{\mathrm{5}} }−{C}_{\mathrm{1}} ^{\mathrm{5}} ×\frac{\mathrm{9}!}{\mathrm{2}^{\mathrm{4}} }+{C}_{\mathrm{2}} ^{\mathrm{5}} ×\frac{\mathrm{8}!}{\mathrm{2}^{\mathrm{3}} }−{C}_{\mathrm{3}} ^{\mathrm{5}} ×\frac{\mathrm{7}!}{\mathrm{2}^{\mathrm{2}} }+{C}_{\mathrm{4}} ^{\mathrm{5}} ×\frac{\mathrm{6}!}{\mathrm{2}}−\mathrm{5}! \\ $$$$=\mathrm{39480} \\ $$
