
Question Number 198207 by a.lgnaoui last updated on 13/Oct/23
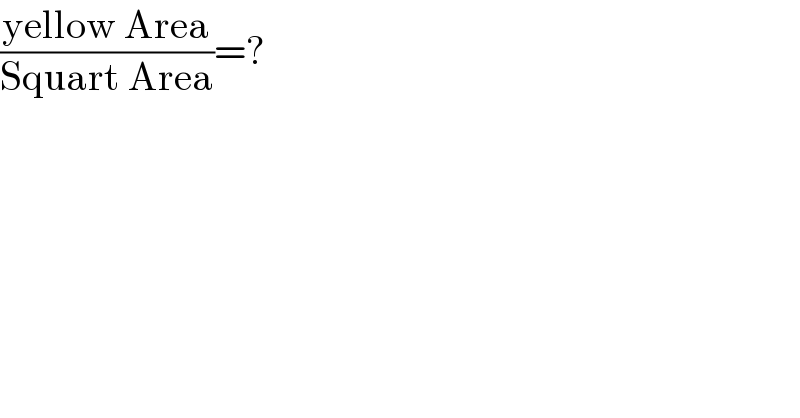
$$\frac{\mathrm{yellow}\:\mathrm{Area}}{\mathrm{Squart}\:\mathrm{Area}}=? \\ $$
Commented by a.lgnaoui last updated on 13/Oct/23
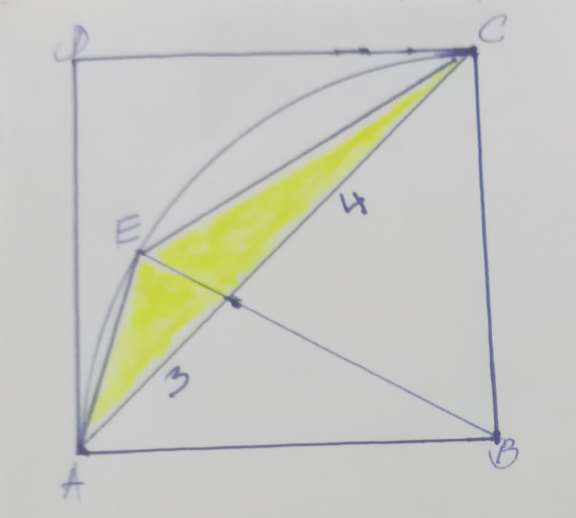
Answered by mr W last updated on 14/Oct/23
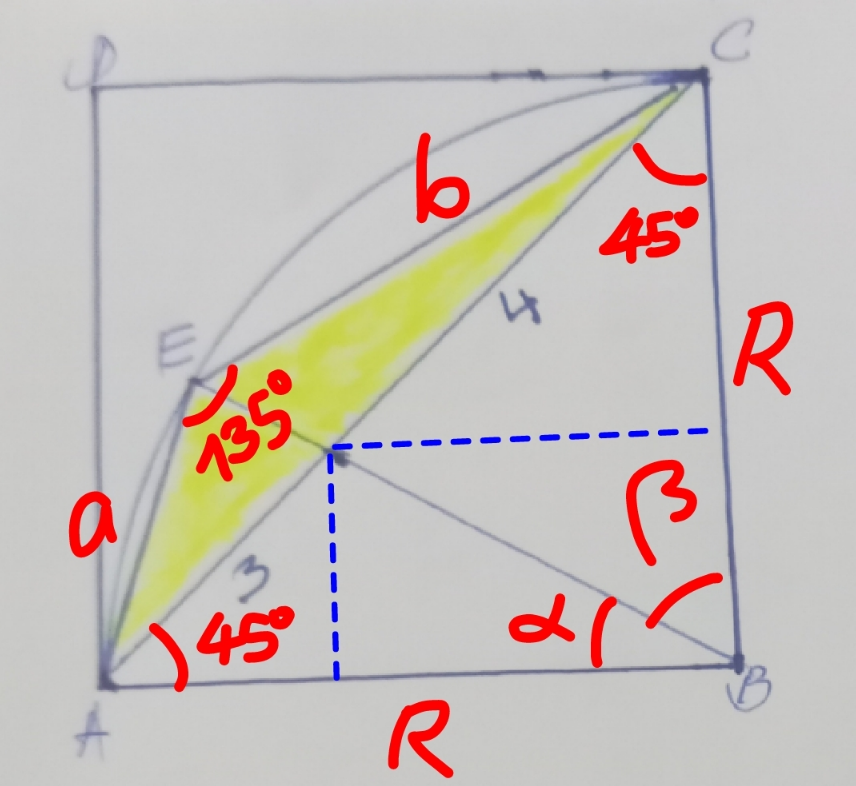
Commented by mr W last updated on 14/Oct/23
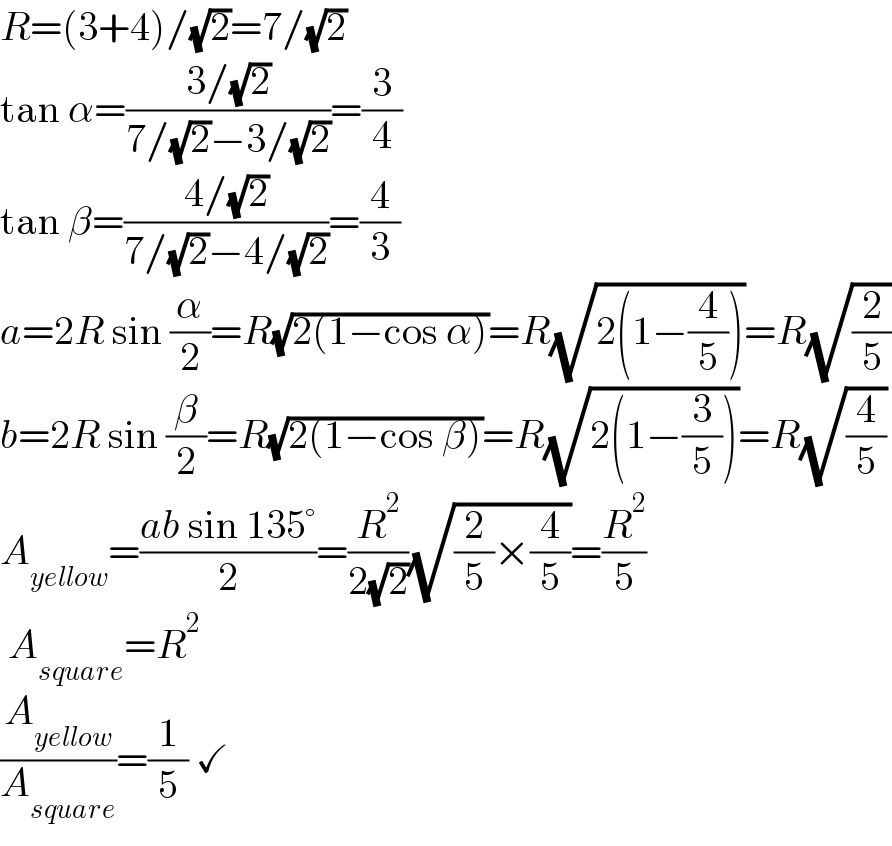
$${R}=\left(\mathrm{3}+\mathrm{4}\right)/\sqrt{\mathrm{2}}=\mathrm{7}/\sqrt{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{3}/\sqrt{\mathrm{2}}}{\mathrm{7}/\sqrt{\mathrm{2}}−\mathrm{3}/\sqrt{\mathrm{2}}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{4}/\sqrt{\mathrm{2}}}{\mathrm{7}/\sqrt{\mathrm{2}}−\mathrm{4}/\sqrt{\mathrm{2}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${a}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}={R}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)}={R}\sqrt{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}\right)}={R}\sqrt{\frac{\mathrm{2}}{\mathrm{5}}} \\ $$$${b}=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}={R}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)}={R}\sqrt{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}\right)}={R}\sqrt{\frac{\mathrm{4}}{\mathrm{5}}} \\ $$$${A}_{{yellow}} =\frac{{ab}\:\mathrm{sin}\:\mathrm{135}°}{\mathrm{2}}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}}\sqrt{\frac{\mathrm{2}}{\mathrm{5}}×\frac{\mathrm{4}}{\mathrm{5}}}=\frac{{R}^{\mathrm{2}} }{\mathrm{5}} \\ $$$$\:{A}_{{square}} ={R}^{\mathrm{2}} \\ $$$$\frac{{A}_{{yellow}} }{{A}_{{square}} }=\frac{\mathrm{1}}{\mathrm{5}}\:\checkmark \\ $$
Commented by a.lgnaoui last updated on 14/Oct/23

$$\mathrm{thanks} \\ $$
