
Previous in Differential Equation Next in Differential Equation
Question Number 120905 by bemath last updated on 03/Nov/20
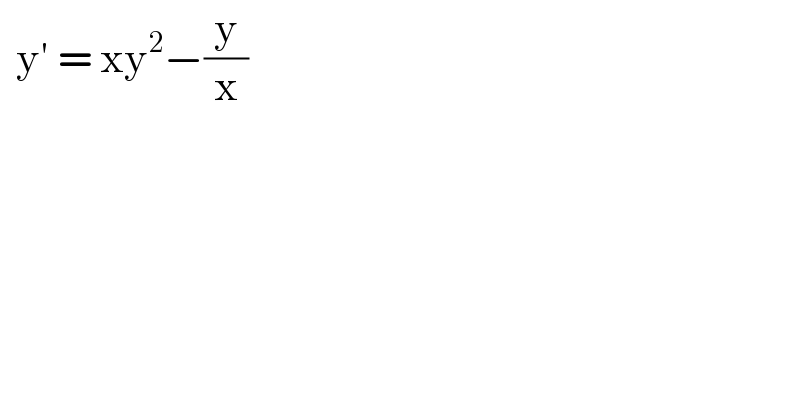
$$\:\:\mathrm{y}'\:=\:\mathrm{xy}^{\mathrm{2}} −\frac{\mathrm{y}}{\mathrm{x}} \\ $$
Answered by Bird last updated on 03/Nov/20
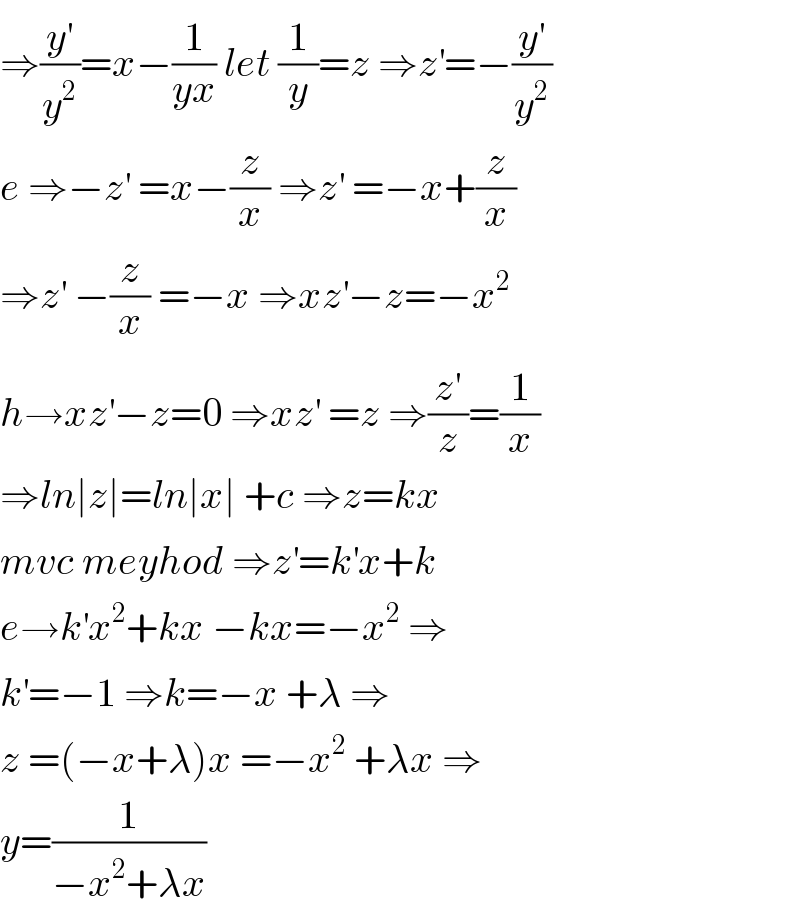
$$\Rightarrow\frac{{y}^{'} }{{y}^{\mathrm{2}} }={x}−\frac{\mathrm{1}}{{yx}}\:{let}\:\frac{\mathrm{1}}{{y}}={z}\:\Rightarrow{z}^{'} =−\frac{{y}^{'} }{{y}^{\mathrm{2}} } \\ $$$${e}\:\Rightarrow−{z}^{'} \:={x}−\frac{{z}}{{x}}\:\Rightarrow{z}^{'} \:=−{x}+\frac{{z}}{{x}} \\ $$$$\Rightarrow{z}^{'} \:−\frac{{z}}{{x}}\:=−{x}\:\Rightarrow{xz}^{'} −{z}=−{x}^{\mathrm{2}} \\ $$$${h}\rightarrow{xz}^{'} −{z}=\mathrm{0}\:\Rightarrow{xz}^{'} \:={z}\:\Rightarrow\frac{{z}^{'} }{{z}}=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{ln}\mid{z}\mid={ln}\mid{x}\mid\:+{c}\:\Rightarrow{z}={kx} \\ $$$${mvc}\:{meyhod}\:\Rightarrow{z}^{'} ={k}^{'} {x}+{k} \\ $$$${e}\rightarrow{k}^{'} {x}^{\mathrm{2}} +{kx}\:−{kx}=−{x}^{\mathrm{2}} \:\Rightarrow \\ $$$${k}^{'} =−\mathrm{1}\:\Rightarrow{k}=−{x}\:+\lambda\:\Rightarrow \\ $$$${z}\:=\left(−{x}+\lambda\right){x}\:=−{x}^{\mathrm{2}} \:+\lambda{x}\:\Rightarrow \\ $$$${y}=\frac{\mathrm{1}}{−{x}^{\mathrm{2}} +\lambda{x}} \\ $$
Answered by bobhans last updated on 04/Nov/20

$$\:{y}'+\frac{{y}}{{x}}\:=\:{xy}^{\mathrm{2}} \\ $$$${let}\:{y}^{−\mathrm{1}} =\:{u}\:\Rightarrow\frac{{du}}{{dx}}\:=\:−{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}} \\ $$$${or}\:\frac{{dy}}{{dx}}\:=\:−{y}^{\mathrm{2}} \:\frac{{du}}{{dx}}\: \\ $$$${substituting}\:{to}\:{diff}\:{equation} \\ $$$${gives}\:−{y}^{\mathrm{2}} \:\frac{{du}}{{dx}}\:+\frac{{y}}{{x}}\:=\:{xy}^{\mathrm{2}} \\ $$$$\Leftrightarrow\frac{{du}}{{dx}}−\frac{{u}}{{x}}\:=−\:{x}\:,\:{put}\:{integrating} \\ $$$${factor}\:{v}\:=\:{e}^{\int\:−\frac{{dx}}{{x}}} =\:{e}^{\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}}\right)} =\frac{\mathrm{1}}{{x}} \\ $$$${multiply}\:{by}\:\frac{\mathrm{1}}{{x}}\:{both}\:{sides} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{{x}}\:\frac{{du}}{{dx}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{u}\:=−\:\mathrm{1}\: \\ $$$$\Leftrightarrow\:\frac{{d}}{{dx}}\left(\frac{{u}}{{x}}\right)\:=\:−\mathrm{1}\:.\:{Integrating}\:{both} \\ $$$${sides}\:{gives}\:\int\:{d}\left(\frac{{u}}{{x}}\right)\:=\:−\int{dx} \\ $$$$\Leftrightarrow\:\frac{{u}}{{x}}\:=\:−{x}+{c}\:\rightarrow\:{u}\:=−\:{x}^{\mathrm{2}} \:+\:{cx}\: \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{{y}}\:=\:−{x}^{\mathrm{2}} +{cx}\:,\:{thus}\:{y}\:=\:\frac{\mathrm{1}}{−{x}^{\mathrm{2}} +{cx}}. \\ $$
Answered by Olaf last updated on 04/Nov/20
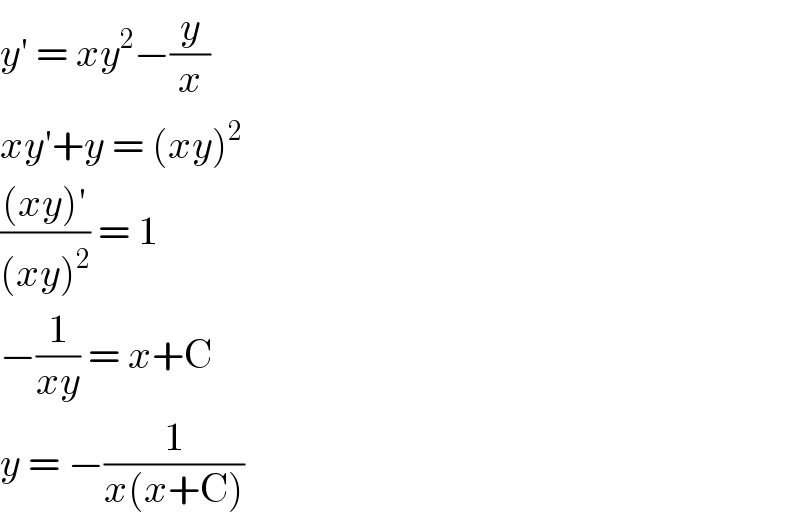
$${y}'\:=\:{xy}^{\mathrm{2}} −\frac{{y}}{{x}} \\ $$$${xy}'+{y}\:=\:\left({xy}\right)^{\mathrm{2}} \\ $$$$\frac{\left({xy}\right)'}{\left({xy}\right)^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$−\frac{\mathrm{1}}{{xy}}\:=\:{x}+\mathrm{C} \\ $$$${y}\:=\:−\frac{\mathrm{1}}{{x}\left({x}+\mathrm{C}\right)} \\ $$
Answered by TANMAY PANACEA last updated on 04/Nov/20
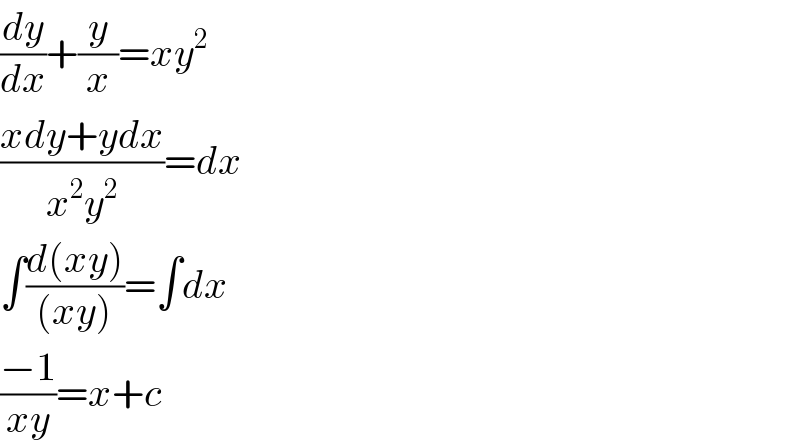
$$\frac{{dy}}{{dx}}+\frac{{y}}{{x}}={xy}^{\mathrm{2}} \\ $$$$\frac{{xdy}+{ydx}}{{x}^{\mathrm{2}} {y}^{\mathrm{2}} }={dx} \\ $$$$\int\frac{{d}\left({xy}\right)}{\left({xy}\right)}=\int{dx} \\ $$$$\frac{−\mathrm{1}}{{xy}}={x}+{c} \\ $$
