
Question Number 178847 by zaheen last updated on 22/Oct/22

$${y}={x}\mathrm{sin}\:\left({x}\right) \\ $$$$\frac{{d}^{\mathrm{35}} {y}}{{dx}^{\mathrm{35}} }=? \\ $$
Answered by mr W last updated on 22/Oct/22
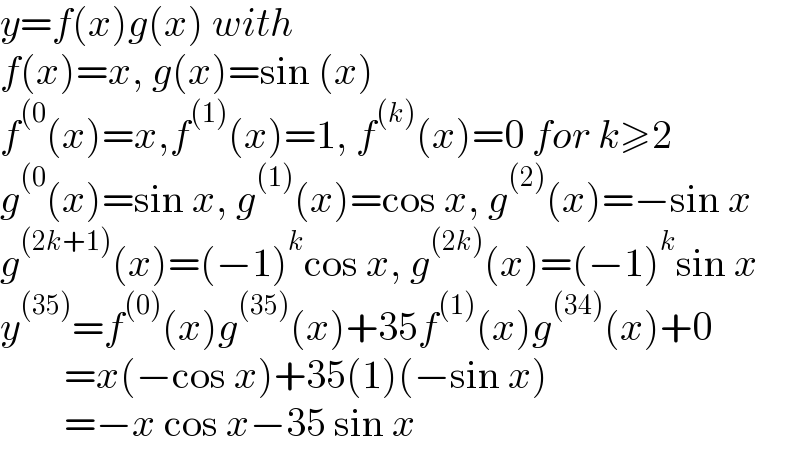
$${y}={f}\left({x}\right){g}\left({x}\right)\:{with} \\ $$$${f}\left({x}\right)={x},\:{g}\left({x}\right)=\mathrm{sin}\:\left({x}\right) \\ $$$${f}^{\left(\mathrm{0}\right.} \left({x}\right)={x},{f}^{\left(\mathrm{1}\right)} \left({x}\right)=\mathrm{1},\:{f}^{\left({k}\right)} \left({x}\right)=\mathrm{0}\:{for}\:{k}\geqslant\mathrm{2} \\ $$$${g}^{\left(\mathrm{0}\right.} \left({x}\right)=\mathrm{sin}\:{x},\:{g}^{\left(\mathrm{1}\right)} \left({x}\right)=\mathrm{cos}\:{x},\:{g}^{\left(\mathrm{2}\right)} \left({x}\right)=−\mathrm{sin}\:{x} \\ $$$${g}^{\left(\mathrm{2}{k}+\mathrm{1}\right)} \left({x}\right)=\left(−\mathrm{1}\right)^{{k}} \mathrm{cos}\:{x},\:{g}^{\left(\mathrm{2}{k}\right)} \left({x}\right)=\left(−\mathrm{1}\right)^{{k}} \mathrm{sin}\:{x} \\ $$$${y}^{\left(\mathrm{35}\right)} ={f}^{\left(\mathrm{0}\right)} \left({x}\right){g}^{\left(\mathrm{35}\right)} \left({x}\right)+\mathrm{35}{f}^{\left(\mathrm{1}\right)} \left({x}\right){g}^{\left(\mathrm{34}\right)} \left({x}\right)+\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:={x}\left(−\mathrm{cos}\:{x}\right)+\mathrm{35}\left(\mathrm{1}\right)\left(−\mathrm{sin}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:=−{x}\:\mathrm{cos}\:{x}−\mathrm{35}\:\mathrm{sin}\:{x} \\ $$
Commented by Tawa11 last updated on 23/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
