
Previous in Differential Equation Next in Differential Equation
Question Number 11597 by tawa last updated on 28/Mar/17
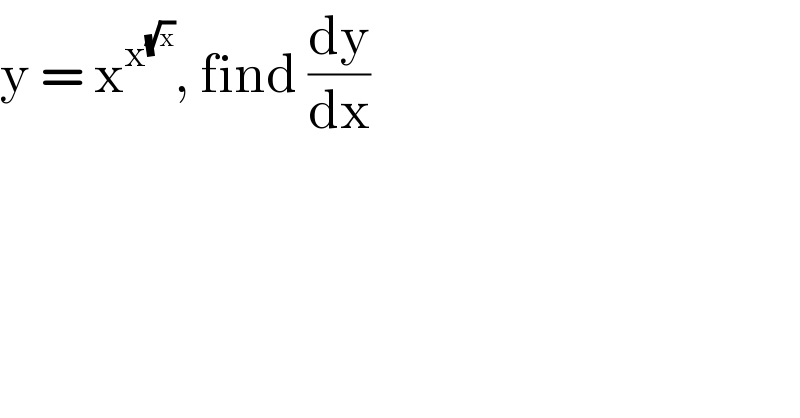
$$\mathrm{y}\:=\:\mathrm{x}^{\mathrm{x}^{\sqrt{\mathrm{x}}} } ,\:\mathrm{find}\:\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$
Answered by sma3l2996 last updated on 28/Mar/17
![y=x^e^((√x)ln(x)) =e^(e^((√x)ln(x)) ln(x)) (dy/dx)=(e^((√x)ln(x)) ln(x))′.e^(e^((√x)ln(x)) ln(x)) =[(e^((√x)ln(x)) )′ln(x)+(ln(x))′e^((√x)ln(x)) ]x^x^(√x) (e^((√x)ln(x)) )′=((√x)ln(x))′e^((√x)ln(x)) =(((ln(x))/(2(√x)))+((√x)/x))x^(√x) so (dy/dx)=[(((ln(x))/(2(√x)))+((√x)/x))x^(√x) ln(x)+(x^(√x) /x)]x^x^(√x) (dy/dx)=[(((ln(x))/(2(√x)))+((√x)/x))ln(x)+(1/x))x^((√x)+x^(√x) )](Q11602.png)
$${y}={x}^{{e}^{\sqrt{{x}}{ln}\left({x}\right)} } ={e}^{{e}^{\sqrt{{x}}{ln}\left({x}\right)} {ln}\left({x}\right)} \\ $$$$\frac{{dy}}{{dx}}=\left({e}^{\sqrt{{x}}{ln}\left({x}\right)} {ln}\left({x}\right)\right)'.{e}^{{e}^{\sqrt{{x}}{ln}\left({x}\right)} {ln}\left({x}\right)} \\ $$$$=\left[\left({e}^{\sqrt{{x}}{ln}\left({x}\right)} \right)'{ln}\left({x}\right)+\left({ln}\left({x}\right)\right)'{e}^{\sqrt{{x}}{ln}\left({x}\right)} \right]{x}^{{x}^{\sqrt{{x}}} } \\ $$$$\left({e}^{\sqrt{{x}}{ln}\left({x}\right)} \right)'=\left(\sqrt{{x}}{ln}\left({x}\right)\right)'{e}^{\sqrt{{x}}{ln}\left({x}\right)} =\left(\frac{{ln}\left({x}\right)}{\mathrm{2}\sqrt{{x}}}+\frac{\sqrt{{x}}}{{x}}\right){x}^{\sqrt{{x}}} \\ $$$${so}\:\frac{{dy}}{{dx}}=\left[\left(\frac{{ln}\left({x}\right)}{\mathrm{2}\sqrt{{x}}}+\frac{\sqrt{{x}}}{{x}}\right){x}^{\sqrt{{x}}} {ln}\left({x}\right)+\frac{{x}^{\sqrt{{x}}} }{{x}}\right]{x}^{{x}^{\sqrt{{x}}} } \\ $$$$\frac{{dy}}{{dx}}=\left[\left(\frac{{ln}\left({x}\right)}{\mathrm{2}\sqrt{{x}}}+\frac{\sqrt{{x}}}{{x}}\right){ln}\left({x}\right)+\frac{\mathrm{1}}{{x}}\right){x}^{\sqrt{{x}}+{x}^{\sqrt{{x}}} } \\ $$
Commented by tawa last updated on 28/Mar/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
