
Question Number 83413 by jagoll last updated on 02/Mar/20

$$\mathrm{y}\:=\:\mathrm{x}\:\mid\mathrm{x}\mid \\ $$$$\mathrm{find}\:\mathrm{y}\:'\:? \\ $$
Commented by mr W last updated on 02/Mar/20
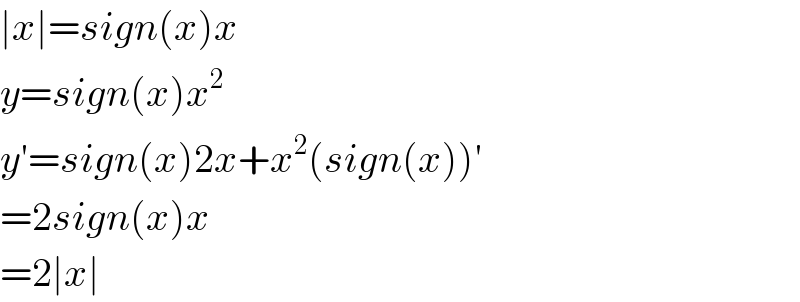
$$\mid{x}\mid={sign}\left({x}\right){x} \\ $$$${y}={sign}\left({x}\right){x}^{\mathrm{2}} \\ $$$${y}'={sign}\left({x}\right)\mathrm{2}{x}+{x}^{\mathrm{2}} \left({sign}\left({x}\right)\right)' \\ $$$$=\mathrm{2}{sign}\left({x}\right){x} \\ $$$$=\mathrm{2}\mid{x}\mid \\ $$
Commented by Kunal12588 last updated on 02/Mar/20
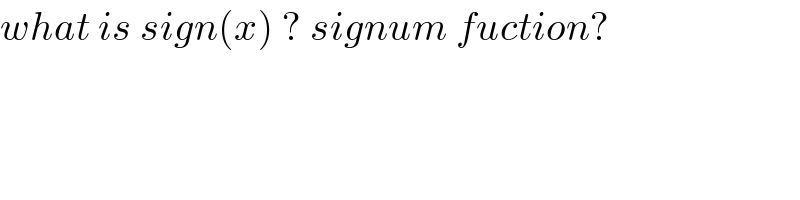
$${what}\:{is}\:{sign}\left({x}\right)\:?\:{signum}\:{fuction}? \\ $$
Commented by mr W last updated on 02/Mar/20
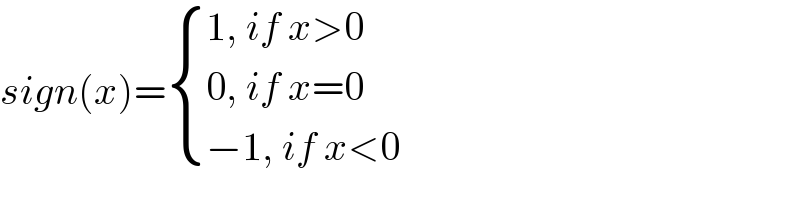
$${sign}\left({x}\right)=\begin{cases}{\mathrm{1},\:{if}\:{x}>\mathrm{0}}\\{\mathrm{0},\:{if}\:{x}=\mathrm{0}}\\{−\mathrm{1},\:{if}\:{x}<\mathrm{0}}\end{cases} \\ $$
Answered by MJS last updated on 02/Mar/20

$${y}=\begin{cases}{−{x}^{\mathrm{2}} ;\:{x}<\mathrm{0}}\\{{x}^{\mathrm{2}} ;\:{x}\geqslant\mathrm{0}}\end{cases} \\ $$$${y}'=\begin{cases}{−\mathrm{2}{x};\:{x}<\mathrm{0}}\\{\mathrm{2}{x};\:{x}\geqslant\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\:{y}'=\mathrm{2}\mid{x}\mid \\ $$
Commented by jagoll last updated on 02/Mar/20
$$\mathrm{yes}...\mathrm{my}\:\mathrm{answer}\:\mathrm{right}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{mister} \\ $$
