
Question Number 193971 by mnjuly1970 last updated on 24/Jun/23
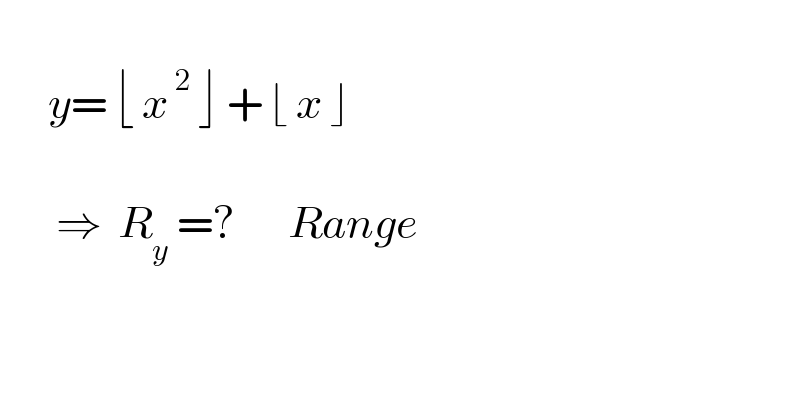
$$ \\ $$$$\:\:\:\:\:\:{y}=\:\lfloor\:{x}^{\:\mathrm{2}} \:\rfloor\:+\:\lfloor\:{x}\:\rfloor\:\: \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\:{R}_{{y}} \:=?\:\:\:\:\:\:\:{Range} \\ $$
Answered by MM42 last updated on 24/Jun/23

$${R}_{{y}} =\left\{−\mathrm{1},\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},...\right\} \\ $$
Answered by mahdipoor last updated on 24/Jun/23
![get x=(√(n^2 +m)) n∈W,0≤m∈R<2n+1 [x^2 ]+[x]=n^2 +[m]+n 0≤[m]<2n+1 R_(y1) ={n^2 +n+m∣n,m∈W,m≤2n} , get x=−(√(n^2 +m))≠0 n∈W,0≤m∈R<2n+1 [x^2 ]+[x]=n^2 +[m]−n−1 0≤[m]<2n+1 R_(y2) ={n^2 −n−1+m∣n,m∈W,m≤2n} , ∩⇒R_y ={r∈Z∣n^2 −n−1≤r≤n^2 +3n,n∈W} for ∀n∈W n^2 +3n≥(n+1)^2 −(n+1)−1 ⇒⇒R_y ={−1,0,1,2,...,∞}](Q193974.png)
$${get}\:\:\:\:{x}=\sqrt{{n}^{\mathrm{2}} +{m}}\:\:\:\:\:\:{n}\in{W},\mathrm{0}\leqslant{m}\in{R}<\mathrm{2}{n}+\mathrm{1} \\ $$$$\left[{x}^{\mathrm{2}} \right]+\left[{x}\right]={n}^{\mathrm{2}} +\left[{m}\right]+{n}\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant\left[{m}\right]<\mathrm{2}{n}+\mathrm{1} \\ $$$${R}_{{y}\mathrm{1}} =\left\{{n}^{\mathrm{2}} +{n}+{m}\mid{n},{m}\in{W},{m}\leqslant\mathrm{2}{n}\right\} \\ $$$$, \\ $$$${get}\:\:\:\:{x}=−\sqrt{{n}^{\mathrm{2}} +{m}}\neq\mathrm{0}\:\:\:\:\:\:{n}\in{W},\mathrm{0}\leqslant{m}\in{R}<\mathrm{2}{n}+\mathrm{1} \\ $$$$\left[{x}^{\mathrm{2}} \right]+\left[{x}\right]={n}^{\mathrm{2}} +\left[{m}\right]−{n}−\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}\leqslant\left[{m}\right]<\mathrm{2}{n}+\mathrm{1} \\ $$$${R}_{{y}\mathrm{2}} =\left\{{n}^{\mathrm{2}} −{n}−\mathrm{1}+{m}\mid{n},{m}\in{W},{m}\leqslant\mathrm{2}{n}\right\} \\ $$$$, \\ $$$$\cap\Rightarrow{R}_{{y}} =\left\{{r}\in{Z}\mid{n}^{\mathrm{2}} −{n}−\mathrm{1}\leqslant{r}\leqslant{n}^{\mathrm{2}} +\mathrm{3}{n},{n}\in{W}\right\} \\ $$$${for}\:\forall{n}\in{W}\:\:\:{n}^{\mathrm{2}} +\mathrm{3}{n}\geqslant\left({n}+\mathrm{1}\right)^{\mathrm{2}} −\left({n}+\mathrm{1}\right)−\mathrm{1} \\ $$$$\Rightarrow\Rightarrow{R}_{{y}} =\left\{−\mathrm{1},\mathrm{0},\mathrm{1},\mathrm{2},...,\infty\right\} \\ $$
