
Question Number 12697 by @ANTARES_VY last updated on 29/Apr/17

$$\boldsymbol{\mathrm{y}}=\mid\boldsymbol{\mathrm{x}}−\mathrm{2}\mid+\mathrm{2}\boldsymbol{\mathrm{x}}−\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\:\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{largest}}\:\:\boldsymbol{\mathrm{values}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{function}}. \\ $$
Answered by mrW1 last updated on 29/Apr/17
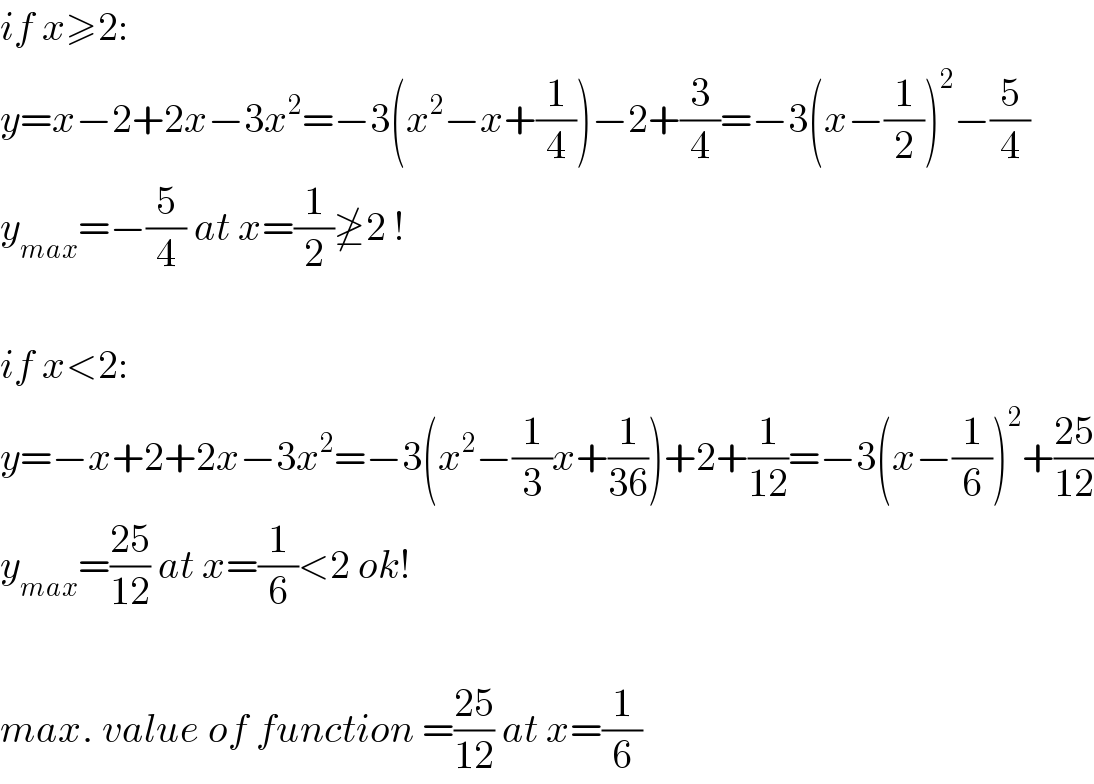
$${if}\:{x}\geqslant\mathrm{2}: \\ $$$${y}={x}−\mathrm{2}+\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} =−\mathrm{3}\left({x}^{\mathrm{2}} −{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{2}+\frac{\mathrm{3}}{\mathrm{4}}=−\mathrm{3}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${y}_{{max}} =−\frac{\mathrm{5}}{\mathrm{4}}\:{at}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\ngeq\mathrm{2}\:! \\ $$$$ \\ $$$${if}\:{x}<\mathrm{2}: \\ $$$${y}=−{x}+\mathrm{2}+\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} =−\mathrm{3}\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}{x}+\frac{\mathrm{1}}{\mathrm{36}}\right)+\mathrm{2}+\frac{\mathrm{1}}{\mathrm{12}}=−\mathrm{3}\left({x}−\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} +\frac{\mathrm{25}}{\mathrm{12}} \\ $$$${y}_{{max}} =\frac{\mathrm{25}}{\mathrm{12}}\:{at}\:{x}=\frac{\mathrm{1}}{\mathrm{6}}<\mathrm{2}\:{ok}! \\ $$$$ \\ $$$${max}.\:{value}\:{of}\:{function}\:=\frac{\mathrm{25}}{\mathrm{12}}\:{at}\:{x}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
