
Question Number 169860 by Shrinava last updated on 11/May/22

$$\mathrm{y}\:=\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1} \\ $$$$\mathrm{y}\:=\:\mathrm{0} \\ $$$$\mathrm{x}\:=\:-\:\mathrm{1} \\ $$$$\mathrm{x}\:=\:\mathrm{2} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{object}\:\mathrm{obtained} \\ $$$$\mathrm{by}\:\mathrm{rotating}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{lines} \\ $$$$\mathrm{around}\:\mathrm{the}\:\mathrm{abscissa}\:\mathrm{axis} \\ $$
Answered by mr W last updated on 11/May/22

Commented by mr W last updated on 11/May/22
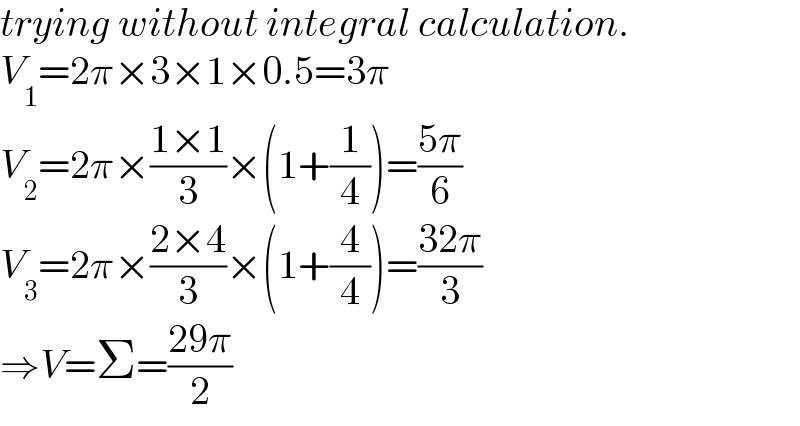
$${trying}\:{without}\:{integral}\:{calculation}. \\ $$$${V}_{\mathrm{1}} =\mathrm{2}\pi×\mathrm{3}×\mathrm{1}×\mathrm{0}.\mathrm{5}=\mathrm{3}\pi \\ $$$${V}_{\mathrm{2}} =\mathrm{2}\pi×\frac{\mathrm{1}×\mathrm{1}}{\mathrm{3}}×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{5}\pi}{\mathrm{6}} \\ $$$${V}_{\mathrm{3}} =\mathrm{2}\pi×\frac{\mathrm{2}×\mathrm{4}}{\mathrm{3}}×\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{4}}\right)=\frac{\mathrm{32}\pi}{\mathrm{3}} \\ $$$$\Rightarrow{V}=\Sigma=\frac{\mathrm{29}\pi}{\mathrm{2}} \\ $$
Commented by Shrinava last updated on 12/May/22
$$\mathrm{Perfect}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
