Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 123667 by sahnaz last updated on 27/Nov/20

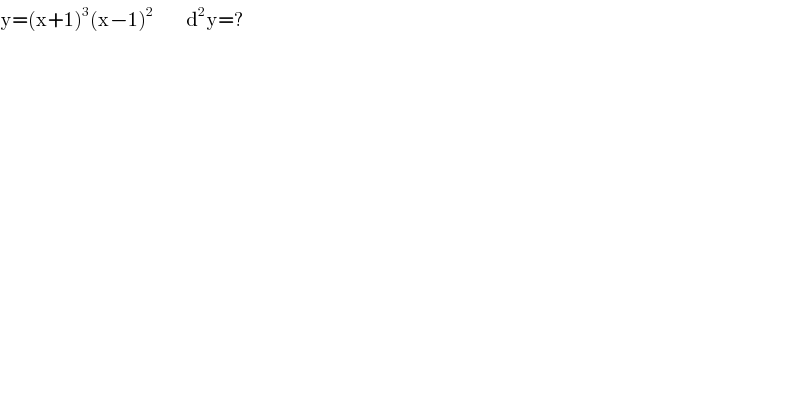
y=(x+1)^3 (x−1)^2 d^2 y=?

$$\mathrm{y}=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\mathrm{d}^{\mathrm{2}} \mathrm{y}=? \\ $$

Answered by mathmax by abdo last updated on 27/Nov/20

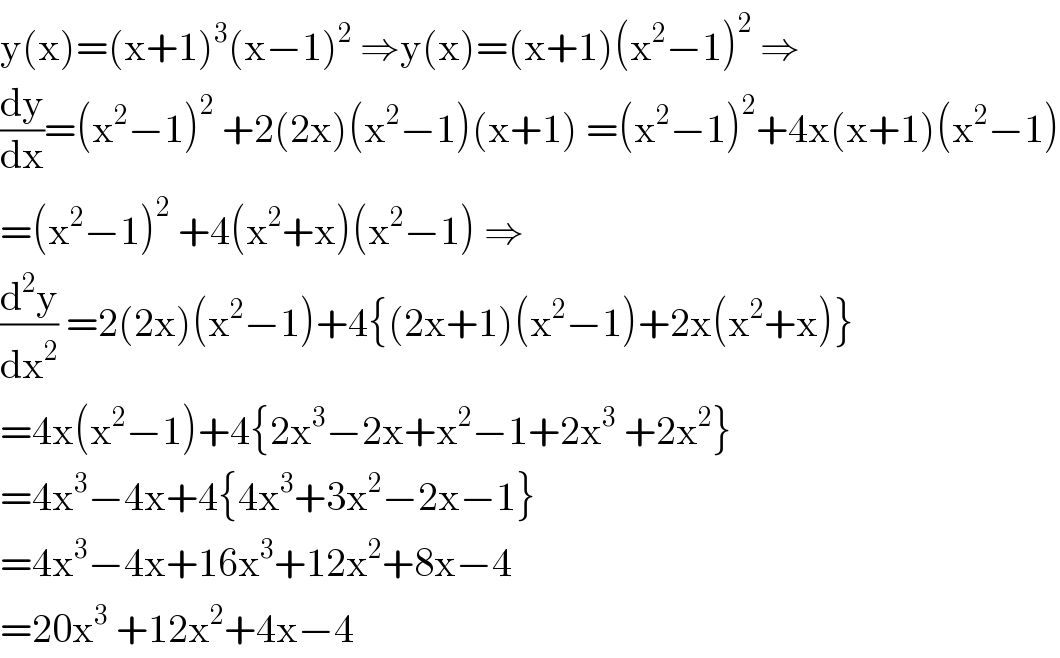
y(x)=(x+1)^3 (x−1)^2 ⇒y(x)=(x+1)(x^2 −1)^2 ⇒ (dy/dx)=(x^2 −1)^2 +2(2x)(x^2 −1)(x+1) =(x^2 −1)^2 +4x(x+1)(x^2 −1) =(x^2 −1)^2 +4(x^2 +x)(x^2 −1) ⇒ (d^2 y/dx^2 ) =2(2x)(x^2 −1)+4{(2x+1)(x^2 −1)+2x(x^2 +x)} =4x(x^2 −1)+4{2x^3 −2x+x^2 −1+2x^3 +2x^2 } =4x^3 −4x+4{4x^3 +3x^2 −2x−1} =4x^3 −4x+16x^3 +12x^2 +8x−4 =20x^3 +12x^2 +4x−4

$$\mathrm{y}\left(\mathrm{x}\right)=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{2x}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)\:=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4x}\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\mathrm{2}\left(\mathrm{2x}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{4}\left\{\left(\mathrm{2x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{2x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\right\} \\ $$$$=\mathrm{4x}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{4}\left\{\mathrm{2x}^{\mathrm{3}} −\mathrm{2x}+\mathrm{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{2x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} \right\} \\ $$$$=\mathrm{4x}^{\mathrm{3}} −\mathrm{4x}+\mathrm{4}\left\{\mathrm{4x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{1}\right\} \\ $$$$=\mathrm{4x}^{\mathrm{3}} −\mathrm{4x}+\mathrm{16x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} +\mathrm{8x}−\mathrm{4} \\ $$$$=\mathrm{20x}^{\mathrm{3}} \:+\mathrm{12x}^{\mathrm{2}} +\mathrm{4x}−\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com