
Question Number 204054 by hardmath last updated on 05/Feb/24
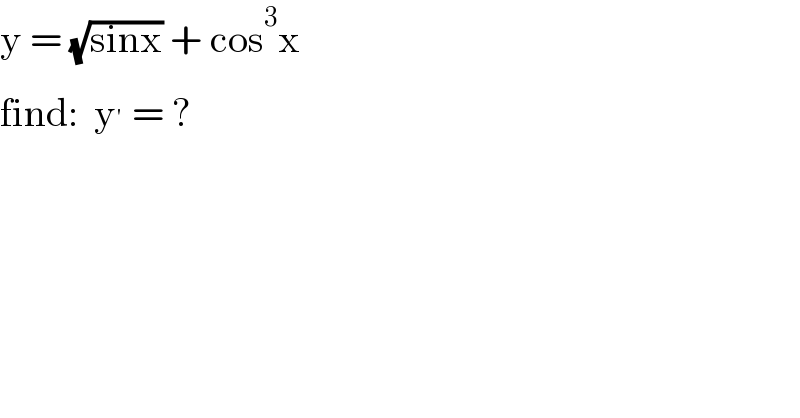
$$\mathrm{y}\:=\:\sqrt{\mathrm{sinx}}\:+\:\mathrm{cos}^{\mathrm{3}} \mathrm{x} \\ $$$$\mathrm{find}:\:\:\mathrm{y}^{'} \:=\:? \\ $$
Answered by deleteduser1 last updated on 05/Feb/24
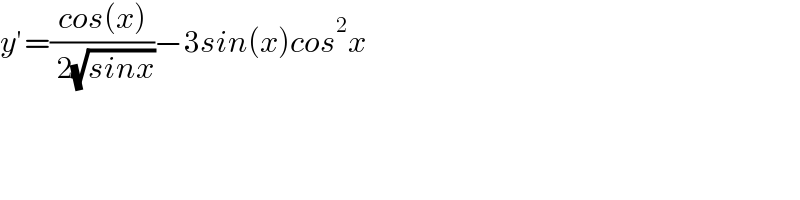
$${y}'=\frac{{cos}\left({x}\right)}{\:\mathrm{2}\sqrt{{sinx}}}−\mathrm{3}{sin}\left({x}\right){cos}^{\mathrm{2}} {x} \\ $$
Answered by Mathspace last updated on 06/Feb/24
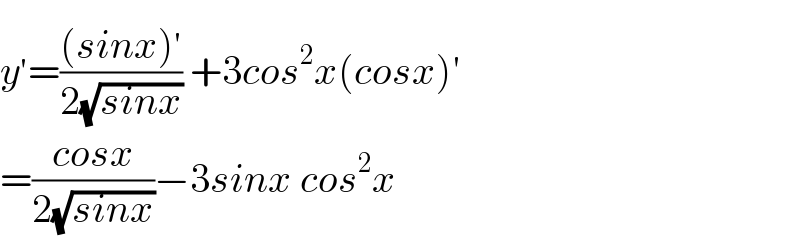
$${y}^{'} =\frac{\left({sinx}\right)^{'} }{\mathrm{2}\sqrt{{sinx}}}\:+\mathrm{3}{cos}^{\mathrm{2}} {x}\left({cosx}\right)' \\ $$$$=\frac{{cosx}}{\mathrm{2}\sqrt{{sinx}}}−\mathrm{3}{sinx}\:{cos}^{\mathrm{2}} {x} \\ $$
