Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 195263 by dimentri last updated on 28/Jul/23

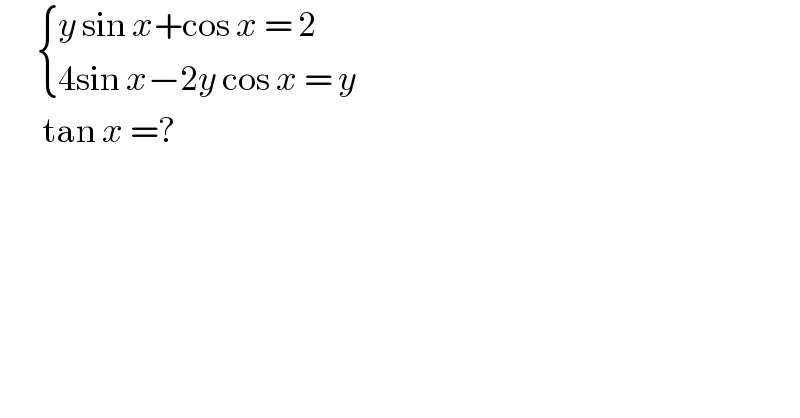
{ ((y sin x+cos x = 2)),((4sin x−2y cos x = y)) :} tan x =?

$$\:\:\:\:\:\:\begin{cases}{{y}\:\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:=\:\mathrm{2}}\\{\mathrm{4sin}\:{x}−\mathrm{2}{y}\:\mathrm{cos}\:{x}\:=\:{y}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\mathrm{tan}\:{x}\:=?\: \\ $$

Answered by cortano12 last updated on 28/Jul/23

{ ( ),( ) :} determinant (( )) { ((4y sin x + 4 cos x = 8)),((4y sin x −2y^2 cos x = y^2 )) :} (4+2y^2 ) cos x = 8−y^2 determinant ((( ((8−y^2 )/(2y^2 +4))))) { ((2y^2 sin x +2y cos x = 4y)),((4 sin x −2y cos x = y)) :} (2y^2 +4) sin x = 5y determinant ((( ((5y)/(2y^2 +4))))) determinant ((( ((5y)/(2y^2 +4)) . ((2y^2 +4)/(8−y^2 ))=((5y)/(8−y^2 )))))

$$\:\:\:\:\:\:\begin{cases}{ }\\{ }\end{cases} \\ $$$$ \\ $$$$ \begin{array}{|c|}{ }\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\begin{cases}{\mathrm{4}{y}\:\mathrm{sin}\:{x}\:+\:\mathrm{4}\:\mathrm{cos}\:{x}\:=\:\mathrm{8}}\\{\mathrm{4}{y}\:\mathrm{sin}\:{x}\:−\mathrm{2}{y}^{\mathrm{2}} \:\mathrm{cos}\:{x}\:=\:{y}^{\mathrm{2}} }\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{4}+\mathrm{2}{y}^{\mathrm{2}} \right)\:\mathrm{cos}\:{x}\:=\:\mathrm{8}−{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\begin{array}{|c|}{ \frac{\mathrm{8}−{y}^{\mathrm{2}} }{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\begin{cases}{\mathrm{2}{y}^{\mathrm{2}} \:\mathrm{sin}\:{x}\:+\mathrm{2}{y}\:\mathrm{cos}\:{x}\:=\:\mathrm{4}{y}}\\{\mathrm{4}\:\mathrm{sin}\:{x}\:−\mathrm{2}{y}\:\mathrm{cos}\:{x}\:=\:{y}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}\right)\:\mathrm{sin}\:{x}\:=\:\mathrm{5}{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\begin{array}{|c|}{ \frac{\mathrm{5}{y}}{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\begin{array}{|c|}{ \frac{\mathrm{5}{y}}{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}}\:.\:\frac{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{4}}{\mathrm{8}−{y}^{\mathrm{2}} }=\frac{\mathrm{5}{y}}{\mathrm{8}−{y}^{\mathrm{2}} }}\\\hline\end{array} \\ $$

Answered by Frix last updated on 28/Jul/23

{ ((y=((2−cos x)/(sin x)))),((y=((4sin x)/(1+2cos x)))) :} ((2−cos x)/(sin x))=((4sin x)/(1+2cos x)) cos^2 x +(3/2)cos x −1=0 cos x =(1/2) [∨cos x =−2] tan x =±((√(1−cos^2 x))/(cos x))=±(√3)

$$\begin{cases}{{y}=\frac{\mathrm{2}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}}\\{{y}=\frac{\mathrm{4sin}\:{x}}{\mathrm{1}+\mathrm{2cos}\:{x}}}\end{cases} \\ $$$$\frac{\mathrm{2}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}=\frac{\mathrm{4sin}\:{x}}{\mathrm{1}+\mathrm{2cos}\:{x}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:{x}\:−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\left[\vee\mathrm{cos}\:{x}\:=−\mathrm{2}\right] \\ $$$$\mathrm{tan}\:{x}\:=\pm\frac{\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}}}{\mathrm{cos}\:{x}}=\pm\sqrt{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com