
Question Number 52820 by 33 last updated on 13/Jan/19
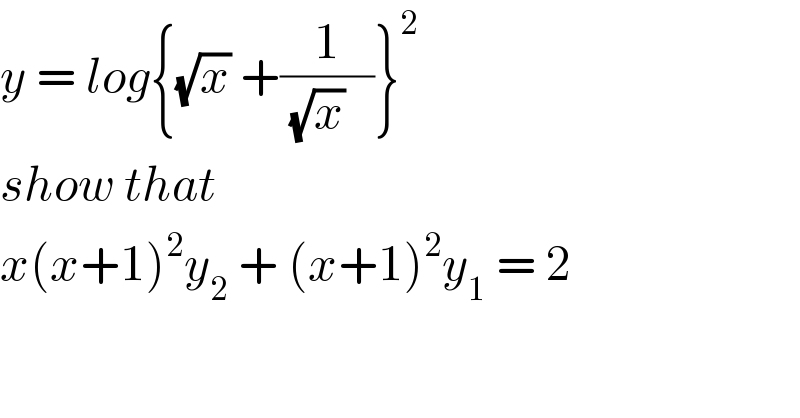
$${y}\:=\:{log}\left\{\sqrt{{x}}\:+\frac{\mathrm{1}}{\sqrt{{x}}\:\:\:}\right\}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${show}\:{that} \\ $$$${x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} {y}_{\mathrm{2}} \:+\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} {y}_{\mathrm{1}} \:=\:\mathrm{2} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jan/19
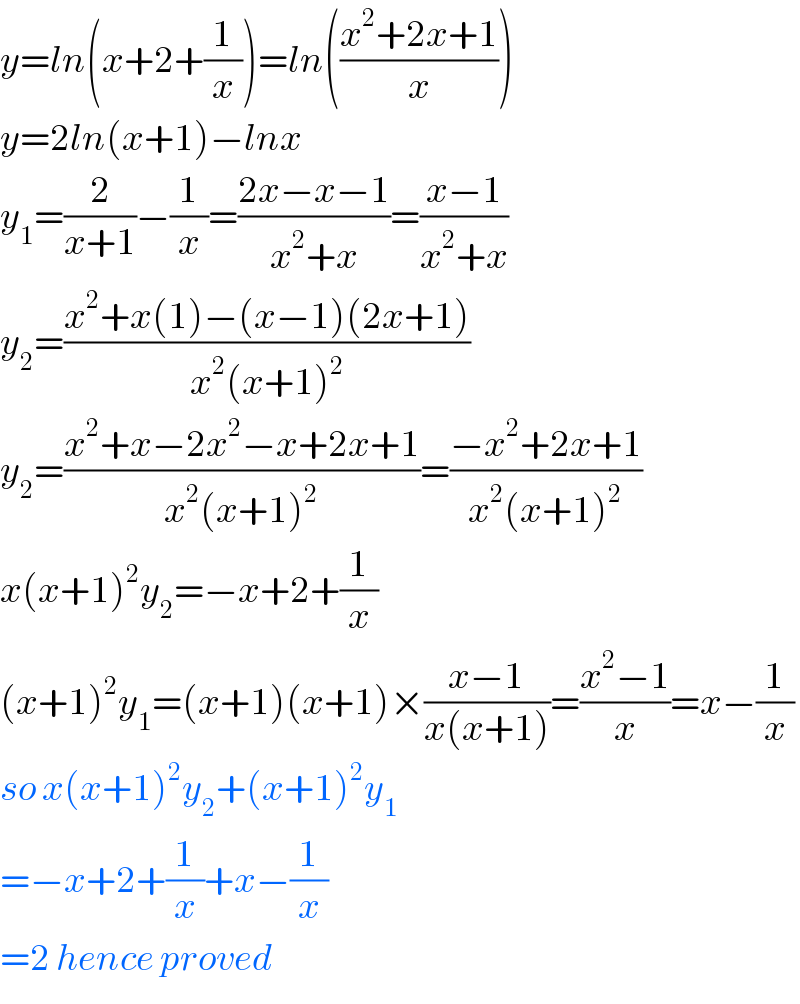
$${y}={ln}\left({x}+\mathrm{2}+\frac{\mathrm{1}}{{x}}\right)={ln}\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}}\right) \\ $$$${y}=\mathrm{2}{ln}\left({x}+\mathrm{1}\right)−{lnx} \\ $$$${y}_{\mathrm{1}} =\frac{\mathrm{2}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}}=\frac{\mathrm{2}{x}−{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}}=\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}} \\ $$$${y}_{\mathrm{2}} =\frac{{x}^{\mathrm{2}} +{x}\left(\mathrm{1}\right)−\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${y}_{\mathrm{2}} =\frac{{x}^{\mathrm{2}} +{x}−\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{−{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} {y}_{\mathrm{2}} =−{x}+\mathrm{2}+\frac{\mathrm{1}}{{x}} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} {y}_{\mathrm{1}} =\left({x}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)×\frac{{x}−\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}}={x}−\frac{\mathrm{1}}{{x}} \\ $$$${so}\:{x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} {y}_{\mathrm{2}} +\left({x}+\mathrm{1}\right)^{\mathrm{2}} {y}_{\mathrm{1}} \\ $$$$=−{x}+\mathrm{2}+\frac{\mathrm{1}}{{x}}+{x}−\frac{\mathrm{1}}{{x}} \\ $$$$=\mathrm{2}\:{hence}\:{proved} \\ $$
Commented by 33 last updated on 14/Jan/19
$${thank}\:{you}\:{so}\:{much} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Jan/19

$${most}\:{welcome}... \\ $$
