
Question Number 47174 by [email protected] last updated on 05/Nov/18
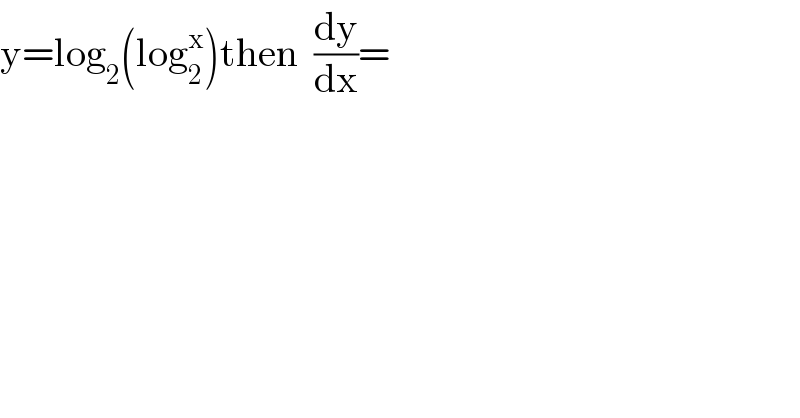
$$\mathrm{y}=\mathrm{log}_{\mathrm{2}} \left(\mathrm{log}_{\mathrm{2}} ^{\mathrm{x}} \right)\mathrm{then}\:\:\frac{\mathrm{dy}}{\mathrm{dx}}= \\ $$
Answered by [email protected] last updated on 05/Nov/18
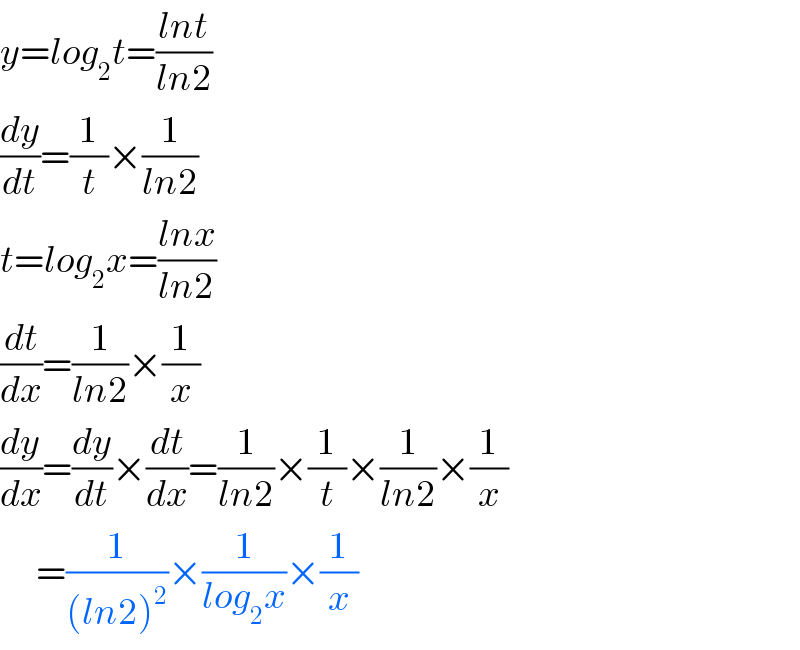
$${y}={log}_{\mathrm{2}} {t}=\frac{{lnt}}{{ln}\mathrm{2}} \\ $$$$\frac{{dy}}{{dt}}=\frac{\mathrm{1}}{{t}}×\frac{\mathrm{1}}{{ln}\mathrm{2}} \\ $$$${t}={log}_{\mathrm{2}} {x}=\frac{{lnx}}{{ln}\mathrm{2}} \\ $$$$\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{ln}\mathrm{2}}×\frac{\mathrm{1}}{{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}×\frac{{dt}}{{dx}}=\frac{\mathrm{1}}{{ln}\mathrm{2}}×\frac{\mathrm{1}}{{t}}×\frac{\mathrm{1}}{{ln}\mathrm{2}}×\frac{\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\left({ln}\mathrm{2}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{{log}_{\mathrm{2}} {x}}×\frac{\mathrm{1}}{{x}} \\ $$
