
Question Number 57284 by Jmasanja last updated on 01/Apr/19

$${y}\:{is}\:{varies}\:{directly}\:{as}\:{the}\:{square}\:{of}\:{x}\:{and} \\ $$$${inversely}\:{as}\:{z}. \\ $$$${if}\:{x}\:{is}\:{inceased}\:{by}\:\mathrm{10\%}\:{and}\:{z}\:\:{is}\: \\ $$$${decreased}\:{by}\:\mathrm{20\%},\:{find}\:{the}\:{percentage} \\ $$$${change}\:{in}\:{y}. \\ $$
Commented by mr W last updated on 01/Apr/19
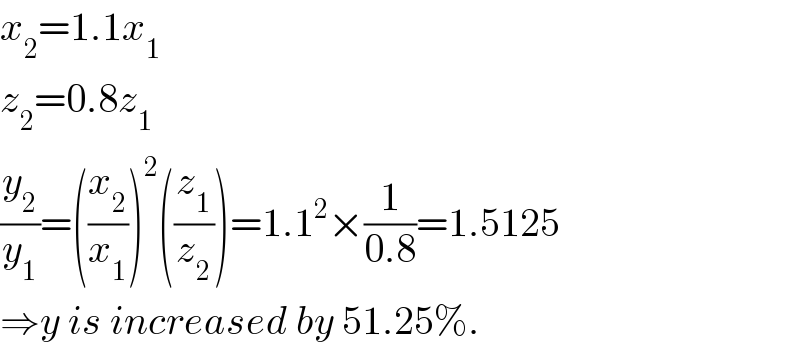
$${x}_{\mathrm{2}} =\mathrm{1}.\mathrm{1}{x}_{\mathrm{1}} \\ $$$${z}_{\mathrm{2}} =\mathrm{0}.\mathrm{8}{z}_{\mathrm{1}} \\ $$$$\frac{{y}_{\mathrm{2}} }{{y}_{\mathrm{1}} }=\left(\frac{{x}_{\mathrm{2}} }{{x}_{\mathrm{1}} }\right)^{\mathrm{2}} \left(\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\right)=\mathrm{1}.\mathrm{1}^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{0}.\mathrm{8}}=\mathrm{1}.\mathrm{5125} \\ $$$$\Rightarrow{y}\:{is}\:{increased}\:{by}\:\mathrm{51}.\mathrm{25\%}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Apr/19
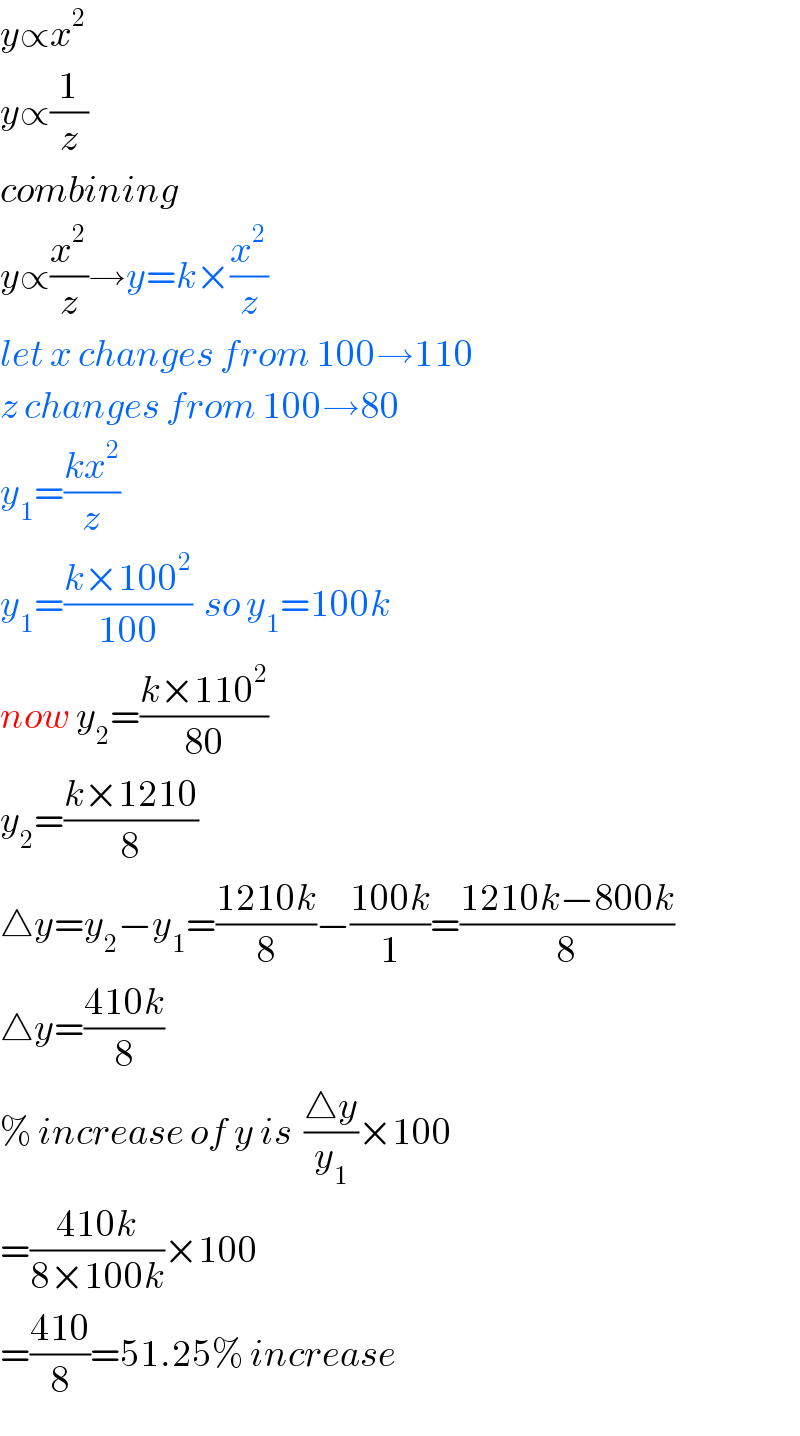
$${y}\propto{x}^{\mathrm{2}} \\ $$$${y}\propto\frac{\mathrm{1}}{{z}} \\ $$$${combining} \\ $$$${y}\propto\frac{{x}^{\mathrm{2}} }{{z}}\rightarrow{y}={k}×\frac{{x}^{\mathrm{2}} }{{z}} \\ $$$${let}\:{x}\:{changes}\:{from}\:\mathrm{100}\rightarrow\mathrm{110} \\ $$$${z}\:{changes}\:{from}\:\mathrm{100}\rightarrow\mathrm{80} \\ $$$${y}_{\mathrm{1}} =\frac{{kx}^{\mathrm{2}} }{{z}} \\ $$$${y}_{\mathrm{1}} =\frac{{k}×\mathrm{100}^{\mathrm{2}} }{\mathrm{100}}\:\:{so}\:{y}_{\mathrm{1}} =\mathrm{100}{k} \\ $$$${now}\:{y}_{\mathrm{2}} =\frac{{k}×\mathrm{110}^{\mathrm{2}} }{\mathrm{80}} \\ $$$${y}_{\mathrm{2}} =\frac{{k}×\mathrm{1210}}{\mathrm{8}} \\ $$$$\bigtriangleup{y}={y}_{\mathrm{2}} −{y}_{\mathrm{1}} =\frac{\mathrm{1210}{k}}{\mathrm{8}}−\frac{\mathrm{100}{k}}{\mathrm{1}}=\frac{\mathrm{1210}{k}−\mathrm{800}{k}}{\mathrm{8}} \\ $$$$\bigtriangleup{y}=\frac{\mathrm{410}{k}}{\mathrm{8}} \\ $$$$\%\:{increase}\:{of}\:{y}\:{is}\:\:\frac{\bigtriangleup{y}}{{y}_{\mathrm{1}} }×\mathrm{100} \\ $$$$=\frac{\mathrm{410}{k}}{\mathrm{8}×\mathrm{100}{k}}×\mathrm{100} \\ $$$$=\frac{\mathrm{410}}{\mathrm{8}}=\mathrm{51}.\mathrm{25\%}\:{increase} \\ $$
