
Question Number 182788 by CrispyXYZ last updated on 14/Dec/22

$${y}''+{ay}={b} \\ $$
Answered by qaz last updated on 14/Dec/22
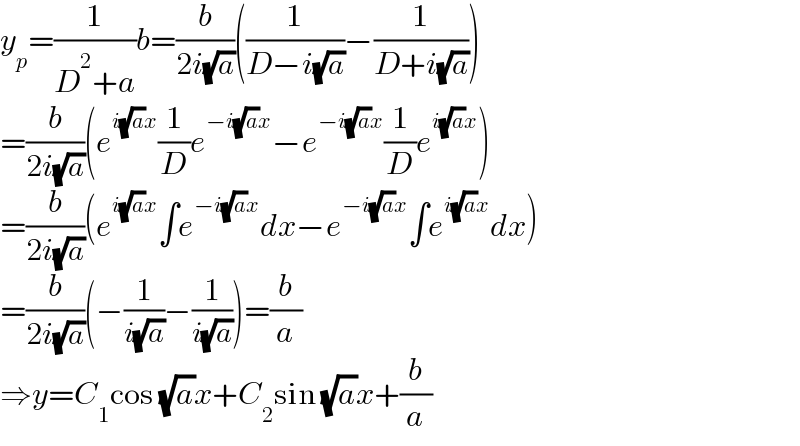
$${y}_{{p}} =\frac{\mathrm{1}}{{D}^{\mathrm{2}} +{a}}{b}=\frac{{b}}{\mathrm{2}{i}\sqrt{{a}}}\left(\frac{\mathrm{1}}{{D}−{i}\sqrt{{a}}}−\frac{\mathrm{1}}{{D}+{i}\sqrt{{a}}}\right) \\ $$$$=\frac{{b}}{\mathrm{2}{i}\sqrt{{a}}}\left({e}^{{i}\sqrt{{a}}{x}} \frac{\mathrm{1}}{{D}}{e}^{−{i}\sqrt{{a}}{x}} −{e}^{−{i}\sqrt{{a}}{x}} \frac{\mathrm{1}}{{D}}{e}^{{i}\sqrt{{a}}{x}} \right) \\ $$$$=\frac{{b}}{\mathrm{2}{i}\sqrt{{a}}}\left({e}^{{i}\sqrt{{a}}{x}} \int{e}^{−{i}\sqrt{{a}}{x}} {dx}−{e}^{−{i}\sqrt{{a}}{x}} \int{e}^{{i}\sqrt{{a}}{x}} {dx}\right) \\ $$$$=\frac{{b}}{\mathrm{2}{i}\sqrt{{a}}}\left(−\frac{\mathrm{1}}{{i}\sqrt{{a}}}−\frac{\mathrm{1}}{{i}\sqrt{{a}}}\right)=\frac{{b}}{{a}} \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} \mathrm{cos}\:\sqrt{{a}}{x}+{C}_{\mathrm{2}} \mathrm{sin}\:\sqrt{{a}}{x}+\frac{{b}}{{a}} \\ $$
