
Previous in Differential Equation Next in Differential Equation
Question Number 91770 by john santu last updated on 03/May/20
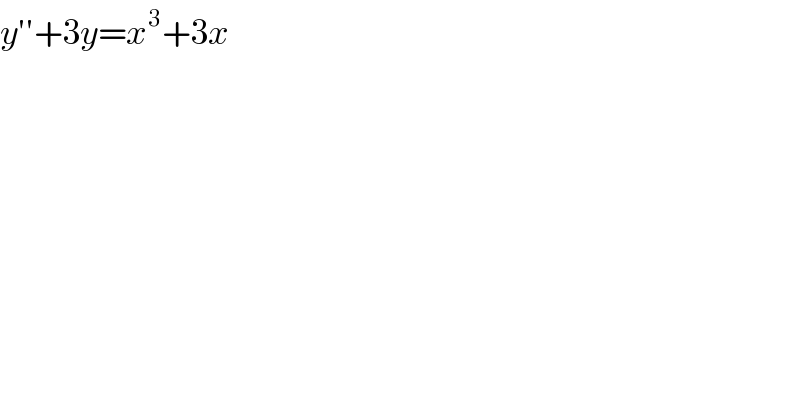
$${y}''+\mathrm{3}{y}={x}^{\mathrm{3}} +\mathrm{3}{x} \\ $$
Commented by Joel578 last updated on 03/May/20
![Let the particular solution is in form y_p = Ax^3 + Bx^2 + Cx + D ⇒ y_p ^′ = 3Ax^2 + 2Bx + C ⇒ y_p ^(′′) = 6Ax + 2B ⇒ y_p ^(′′) + 3y_p = [6Ax + 2B] + 3[Ax^3 + Bx^2 + Cx + D] = 3Ax^3 + 3Bx^2 + (6A+3C)x + (2B+3D) = x^3 + 3x Comparing coeff. on both sides,we get A = (1/3), B = 0, C = (1/3), D = 0 Complete solution y = c_1 cos ((√3)x) + c_2 sin ((√3)x) + (1/3)x^3 + (1/3)x](Q91873.png)
$$\mathrm{Let}\:\mathrm{the}\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{in}\:\mathrm{form} \\ $$$${y}_{{p}} \:=\:{Ax}^{\mathrm{3}} \:+\:{Bx}^{\mathrm{2}} \:+\:{Cx}\:+\:{D} \\ $$$$\Rightarrow\:{y}_{{p}} ^{'} \:=\:\mathrm{3}{Ax}^{\mathrm{2}} \:+\:\mathrm{2}{Bx}\:+\:{C} \\ $$$$\Rightarrow\:{y}_{{p}} ^{''} \:=\:\mathrm{6}{Ax}\:+\:\mathrm{2}{B} \\ $$$$ \\ $$$$\Rightarrow\:{y}_{{p}} ^{''} \:+\:\mathrm{3}{y}_{{p}} \:=\:\left[\mathrm{6}{Ax}\:+\:\mathrm{2}{B}\right]\:+\:\mathrm{3}\left[{Ax}^{\mathrm{3}} \:+\:{Bx}^{\mathrm{2}} \:+\:{Cx}\:+\:{D}\right] \\ $$$$\:\:\:\:\:=\:\mathrm{3}{Ax}^{\mathrm{3}} \:+\:\mathrm{3}{Bx}^{\mathrm{2}} \:+\:\left(\mathrm{6}{A}+\mathrm{3}{C}\right){x}\:+\:\left(\mathrm{2}{B}+\mathrm{3}{D}\right)\:=\:{x}^{\mathrm{3}} \:+\:\mathrm{3}{x} \\ $$$$\mathrm{Comparing}\:\mathrm{coeff}.\:\mathrm{on}\:\mathrm{both}\:\mathrm{sides},\mathrm{we}\:\mathrm{get} \\ $$$${A}\:=\:\frac{\mathrm{1}}{\mathrm{3}},\:{B}\:=\:\mathrm{0},\:{C}\:=\:\frac{\mathrm{1}}{\mathrm{3}},\:{D}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Complete}\:\mathrm{solution} \\ $$$${y}\:=\:{c}_{\mathrm{1}} \:\mathrm{cos}\:\left(\sqrt{\mathrm{3}}{x}\right)\:+\:{c}_{\mathrm{2}} \:\mathrm{sin}\:\left(\sqrt{\mathrm{3}}{x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} \:+\:\frac{\mathrm{1}}{\mathrm{3}}{x} \\ $$
Commented by john santu last updated on 03/May/20

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
Answered by niroj last updated on 03/May/20
 = (1/3)(1−(D^2 /3)+(D^3 /3))(x^3 +3x) = (1/3)[(x^3 +3x)−(1/3).18x+(1/3)18] = (1/3)[x^3 +3x−6x+6] = (1/3)(x^3 −3x+6) y=Acos(√3) x+Bsin(√2) x+(1/3)(x^3 −3x+6)//.](Q91777.png)
$$\:\:\mathrm{y}^{''} +\mathrm{3y}=\mathrm{x}^{\mathrm{3}} +\mathrm{3x} \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{3y}=\mathrm{x}^{\mathrm{3}} +\mathrm{3x} \\ $$$$\:\:\:\left(\mathrm{D}^{\mathrm{2}} +\mathrm{3}\right)\mathrm{y}=\mathrm{x}^{\mathrm{3}} +\mathrm{3x} \\ $$$$\:\:\:\:\mathrm{A}.\mathrm{E}.,\:\:\mathrm{m}^{\mathrm{2}} +\mathrm{3} \\ $$$$\:\:\mathrm{m}=\:\mathrm{0}\overset{−} {+}\sqrt{\mathrm{3}}\:\:\mathrm{i} \\ $$$$\:\:\mathrm{CF}=\:\mathrm{A}\:\mathrm{cos}\sqrt{\mathrm{3}}\:\mathrm{x}+\mathrm{Bsin}\sqrt{\mathrm{3}}\:\:\mathrm{x} \\ $$$$\:\mathrm{PI}=\:\:\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{3x}}{\mathrm{D}^{\mathrm{2}} +\mathrm{3}}=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{D}^{\mathrm{2}} }{\mathrm{3}}}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}\right) \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{D}^{\mathrm{2}} }{\mathrm{3}}\right)^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}\right) \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{1}−\frac{\mathrm{D}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{D}^{\mathrm{3}} }{\mathrm{3}}−..\right]\left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}\right) \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{D}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{D}^{\mathrm{3}} }{\mathrm{3}}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}\right)−\frac{\mathrm{1}}{\mathrm{3}}.\mathrm{18x}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{18}\right] \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{6x}+\mathrm{6}\right] \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{3x}+\mathrm{6}\right) \\ $$$$\:\mathrm{y}=\mathrm{Acos}\sqrt{\mathrm{3}}\:\mathrm{x}+\mathrm{Bsin}\sqrt{\mathrm{2}}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{3x}+\mathrm{6}\right)//. \\ $$
Commented by john santu last updated on 03/May/20

$${fantastic}\: \\ $$
Commented by niroj last updated on 03/May/20
��
Commented by abdomathmax last updated on 03/May/20
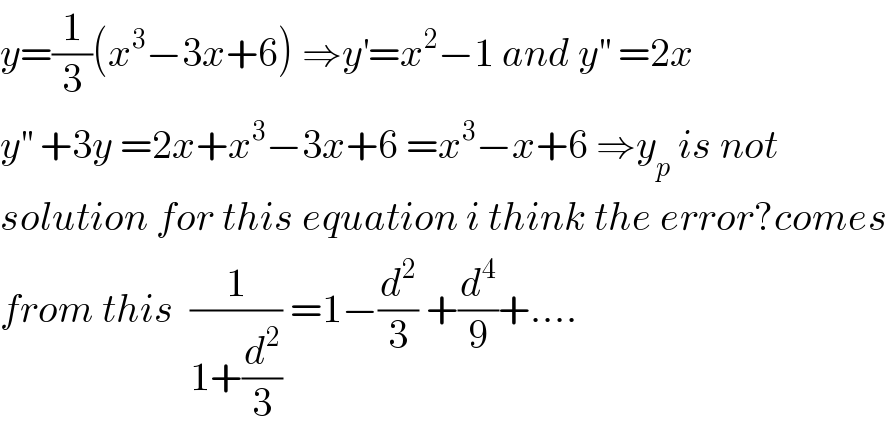
$${y}=\frac{\mathrm{1}}{\mathrm{3}}\left({x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{6}\right)\:\Rightarrow{y}^{'} ={x}^{\mathrm{2}} −\mathrm{1}\:{and}\:{y}^{''} \:=\mathrm{2}{x} \\ $$$${y}^{''} \:+\mathrm{3}{y}\:=\mathrm{2}{x}+{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{6}\:={x}^{\mathrm{3}} −{x}+\mathrm{6}\:\Rightarrow{y}_{{p}} \:{is}\:{not} \\ $$$${solution}\:{for}\:{this}\:{equation}\:{i}\:{think}\:{the}\:{error}?{comes} \\ $$$${from}\:{this}\:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{{d}^{\mathrm{2}} }{\mathrm{3}}}\:=\mathrm{1}−\frac{{d}^{\mathrm{2}} }{\mathrm{3}}\:+\frac{{d}^{\mathrm{4}} }{\mathrm{9}}+.... \\ $$
Commented by niroj last updated on 03/May/20
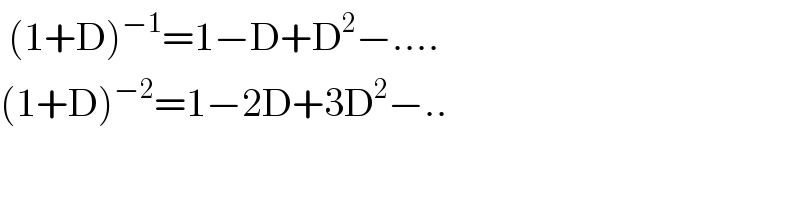
$$\:\left(\mathrm{1}+\mathrm{D}\right)^{−\mathrm{1}} =\mathrm{1}−\mathrm{D}+\mathrm{D}^{\mathrm{2}} −.... \\ $$$$\left(\mathrm{1}+\mathrm{D}\right)^{−\mathrm{2}} =\mathrm{1}−\mathrm{2D}+\mathrm{3D}^{\mathrm{2}} −.. \\ $$
