
Previous in Differential Equation Next in Differential Equation
Question Number 27028 by sorour87 last updated on 01/Jan/18
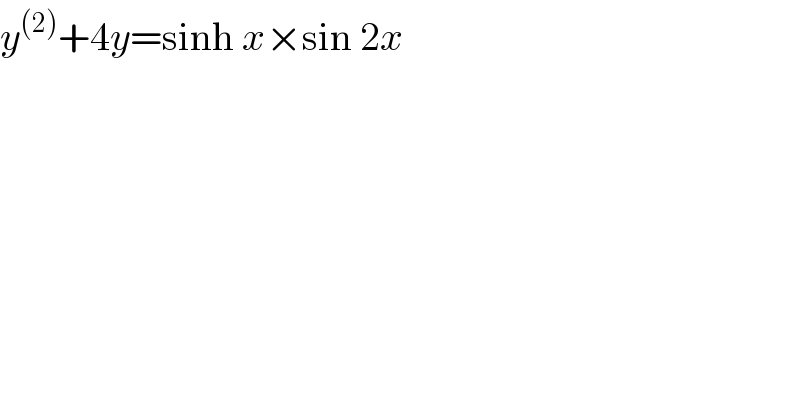
$${y}^{\left(\mathrm{2}\right)} +\mathrm{4}{y}=\mathrm{sinh}\:{x}×\mathrm{sin}\:\mathrm{2}{x} \\ $$
Answered by prakash jain last updated on 02/Jan/18
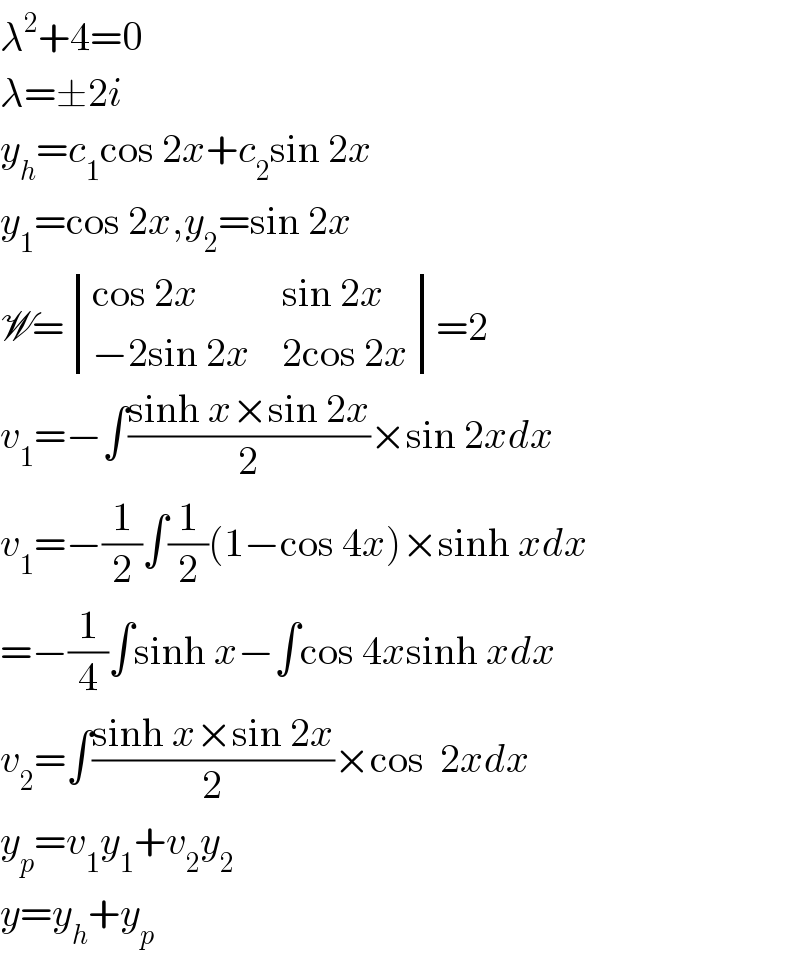
$$\lambda^{\mathrm{2}} +\mathrm{4}=\mathrm{0} \\ $$$$\lambda=\pm\mathrm{2}{i} \\ $$$${y}_{{h}} ={c}_{\mathrm{1}} \mathrm{cos}\:\mathrm{2}{x}+{c}_{\mathrm{2}} \mathrm{sin}\:\mathrm{2}{x} \\ $$$${y}_{\mathrm{1}} =\mathrm{cos}\:\mathrm{2}{x},{y}_{\mathrm{2}} =\mathrm{sin}\:\mathrm{2}{x} \\ $$$$\mathscr{W}=\begin{vmatrix}{\mathrm{cos}\:\mathrm{2}{x}}&{\mathrm{sin}\:\mathrm{2}{x}}\\{−\mathrm{2sin}\:\mathrm{2}{x}}&{\mathrm{2cos}\:\mathrm{2}{x}}\end{vmatrix}=\mathrm{2} \\ $$$${v}_{\mathrm{1}} =−\int\frac{\mathrm{sinh}\:{x}×\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}×\mathrm{sin}\:\mathrm{2}{xdx} \\ $$$${v}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}\right)×\mathrm{sinh}\:{xdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{sinh}\:{x}−\int\mathrm{cos}\:\mathrm{4}{x}\mathrm{sinh}\:{xdx} \\ $$$${v}_{\mathrm{2}} =\int\frac{\mathrm{sinh}\:{x}×\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}×\mathrm{cos}\:\:\mathrm{2}{xdx} \\ $$$${y}_{{p}} ={v}_{\mathrm{1}} {y}_{\mathrm{1}} +{v}_{\mathrm{2}} {y}_{\mathrm{2}} \\ $$$${y}={y}_{{h}} +{y}_{{p}} \\ $$
