Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188407 by HeferH last updated on 01/Mar/23

xf(x) = f(x + 2) f(2) = 2 f(8) = ?

$${xf}\left({x}\right)\:=\:{f}\left({x}\:+\:\mathrm{2}\right) \\ $$$${f}\left(\mathrm{2}\right)\:=\:\mathrm{2} \\ $$$${f}\left(\mathrm{8}\right)\:=\:?\: \\ $$

Answered by horsebrand11 last updated on 01/Mar/23

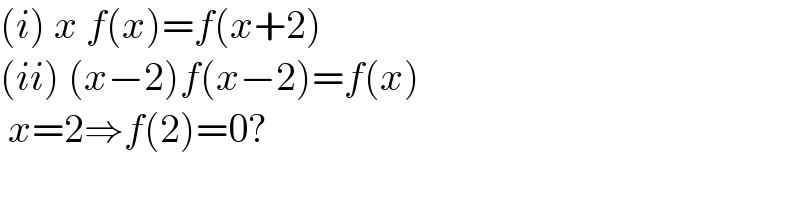
(i) x f(x)=f(x+2) (ii) (x−2)f(x−2)=f(x) x=2⇒f(2)=0?

$$\left({i}\right)\:{x}\:{f}\left({x}\right)={f}\left({x}+\mathrm{2}\right) \\ $$$$\left({ii}\right)\:\left({x}−\mathrm{2}\right){f}\left({x}−\mathrm{2}\right)={f}\left({x}\right) \\ $$$$\:{x}=\mathrm{2}\Rightarrow{f}\left(\mathrm{2}\right)=\mathrm{0}?\:\: \\ $$

Answered by manxsol last updated on 01/Mar/23

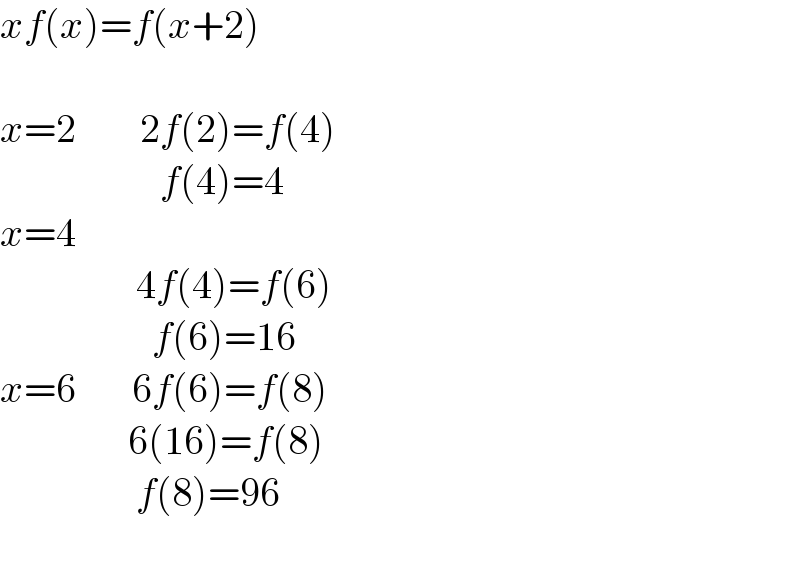
xf(x)=f(x+2) x=2 2f(2)=f(4) f(4)=4 x=4 4f(4)=f(6) f(6)=16 x=6 6f(6)=f(8) 6(16)=f(8) f(8)=96

$${xf}\left({x}\right)={f}\left({x}+\mathrm{2}\right) \\ $$$$ \\ $$$${x}=\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{2}{f}\left(\mathrm{2}\right)={f}\left(\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\mathrm{4}\right)=\mathrm{4} \\ $$$${x}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{f}\left(\mathrm{4}\right)={f}\left(\mathrm{6}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\mathrm{6}\right)=\mathrm{16} \\ $$$${x}=\mathrm{6}\:\:\:\:\:\:\:\mathrm{6}{f}\left(\mathrm{6}\right)={f}\left(\mathrm{8}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}\left(\mathrm{16}\right)={f}\left(\mathrm{8}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\mathrm{8}\right)=\mathrm{96} \\ $$$$ \\ $$

Commented by mr W last updated on 01/Mar/23

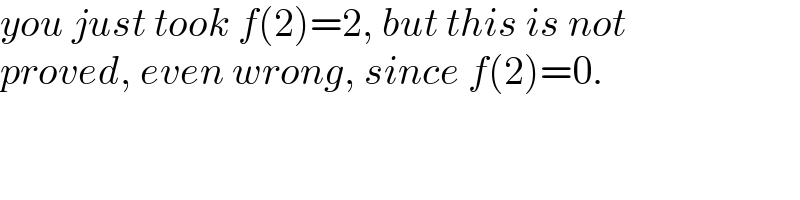
you just took f(2)=2, but this is not proved, even wrong, since f(2)=0.

$${you}\:{just}\:{took}\:{f}\left(\mathrm{2}\right)=\mathrm{2},\:{but}\:{this}\:{is}\:{not} \\ $$$${proved},\:{even}\:{wrong},\:{since}\:{f}\left(\mathrm{2}\right)=\mathrm{0}. \\ $$

Answered by mr W last updated on 01/Mar/23

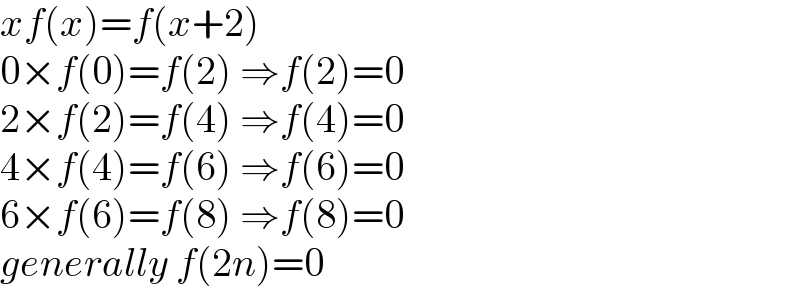
xf(x)=f(x+2) 0×f(0)=f(2) ⇒f(2)=0 2×f(2)=f(4) ⇒f(4)=0 4×f(4)=f(6) ⇒f(6)=0 6×f(6)=f(8) ⇒f(8)=0 generally f(2n)=0

$${xf}\left({x}\right)={f}\left({x}+\mathrm{2}\right) \\ $$$$\mathrm{0}×{f}\left(\mathrm{0}\right)={f}\left(\mathrm{2}\right)\:\Rightarrow{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{2}×{f}\left(\mathrm{2}\right)={f}\left(\mathrm{4}\right)\:\Rightarrow{f}\left(\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{4}×{f}\left(\mathrm{4}\right)={f}\left(\mathrm{6}\right)\:\Rightarrow{f}\left(\mathrm{6}\right)=\mathrm{0} \\ $$$$\mathrm{6}×{f}\left(\mathrm{6}\right)={f}\left(\mathrm{8}\right)\:\Rightarrow{f}\left(\mathrm{8}\right)=\mathrm{0} \\ $$$${generally}\:{f}\left(\mathrm{2}{n}\right)=\mathrm{0} \\ $$

Commented by manxsol last updated on 01/Mar/23

dato f(2)=2 0×f(0)=f(2)⇒f(2)=0 f(2) has two imagen⇒f no is funtion. i am worked with funtion not with relation

$${dato}\:{f}\left(\mathrm{2}\right)=\mathrm{2} \\ $$$$\mathrm{0}×{f}\left(\mathrm{0}\right)={f}\left(\mathrm{2}\right)\Rightarrow{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)\:{has}\:{two} \\ $$$$\:{imagen}\Rightarrow{f}\:{no}\:{is}\:{funtion}. \\ $$$${i}\:{am}\:{worked}\:{with}\:{funtion} \\ $$$$\:{not}\:{with}\:{relation} \\ $$$$ \\ $$

Commented by manxsol last updated on 01/Mar/23

0 cannot be in the domain of the given funtion.the function goes through (2,2). I dont have to try it .

$$\mathrm{0}\:{cannot}\:{be}\:{in}\:{the}\:{domain}\: \\ $$$${of}\:{the}\:{given}\:{funtion}.{the} \\ $$$$\:{function}\:{goes}\:{through}\:\left(\mathrm{2},\mathrm{2}\right). \\ $$$${I}\:{dont}\:{have}\:{to}\:{try}\:{it}\:. \\ $$

Commented by mr W last updated on 01/Mar/23

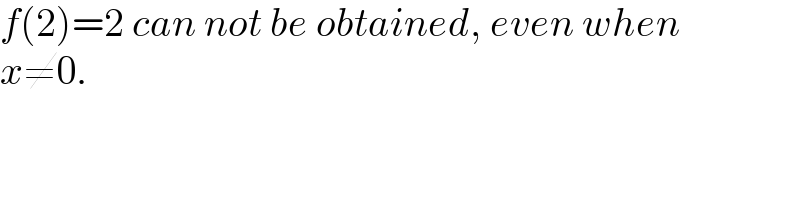
f(2)=2 can not be obtained, even when x≠0.

$${f}\left(\mathrm{2}\right)=\mathrm{2}\:{can}\:{not}\:{be}\:{obtained},\:{even}\:{when} \\ $$$${x}\neq\mathrm{0}. \\ $$

Commented by manxsol last updated on 01/Mar/23

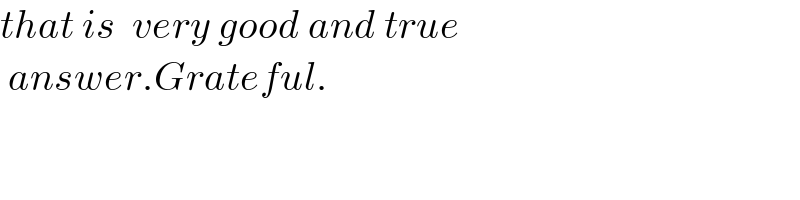
that is very good and true answer.Grateful.

$${that}\:{is}\:\:{very}\:{good}\:{and}\:{true} \\ $$$$\:{answer}.{Grateful}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com