
Question Number 184346 by Matica last updated on 05/Jan/23
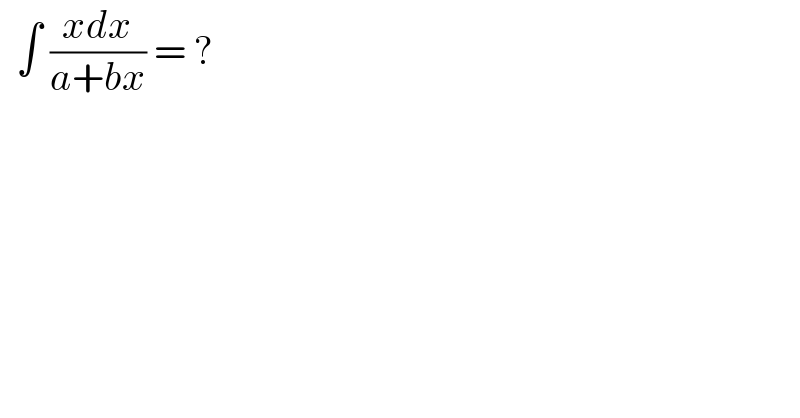
$$\:\:\int\:\frac{{xdx}}{{a}+{bx}}\:=\:? \\ $$
Answered by SEKRET last updated on 05/Jan/23
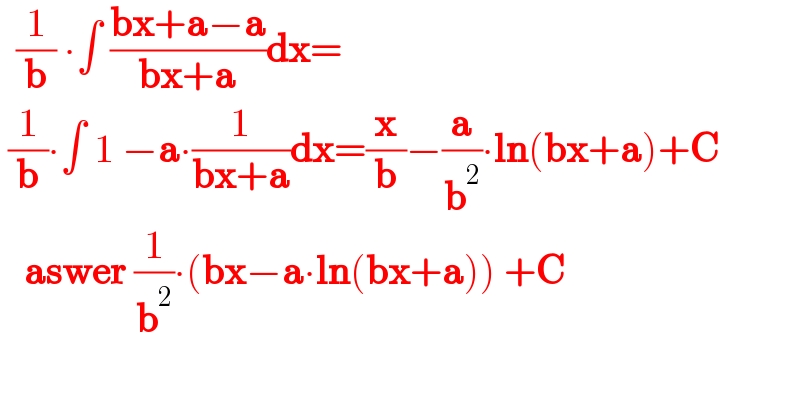
$$\:\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{b}}}\:\centerdot\int\:\frac{\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{a}}−\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{a}}}\boldsymbol{\mathrm{dx}}= \\ $$$$\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{b}}}\centerdot\int\:\mathrm{1}\:−\boldsymbol{\mathrm{a}}\centerdot\frac{\mathrm{1}}{\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{a}}}\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{b}}}−\frac{\boldsymbol{\mathrm{a}}}{\boldsymbol{\mathrm{b}}^{\mathrm{2}} }\centerdot\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{a}}\right)+\boldsymbol{\mathrm{C}} \\ $$$$\:\:\:\boldsymbol{\mathrm{aswer}}\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{b}}^{\mathrm{2}} }\centerdot\left(\boldsymbol{\mathrm{bx}}−\boldsymbol{\mathrm{a}}\centerdot\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{a}}\right)\right)\:+\boldsymbol{\mathrm{C}} \\ $$$$ \\ $$
