
Question Number 194105 by York12 last updated on 27/Jun/23
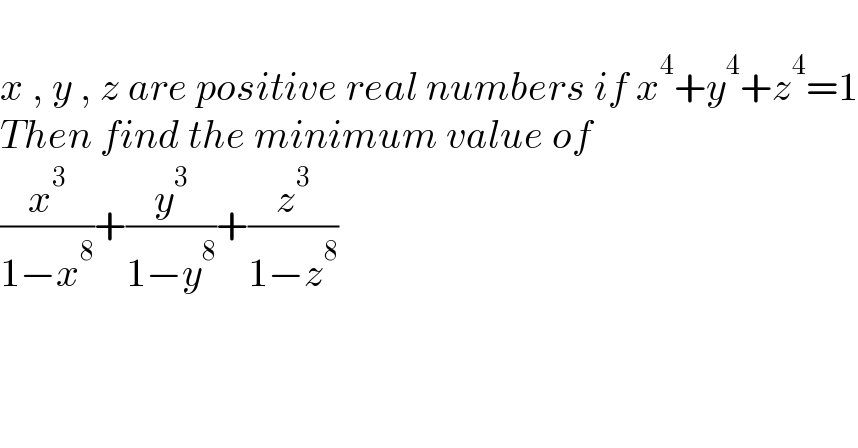
$$ \\ $$$${x}\:,\:{y}\:,\:{z}\:{are}\:{positive}\:{real}\:{numbers}\:{if}\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{1} \\ $$$${Then}\:{find}\:{the}\:{minimum}\:{value}\:{of}\: \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{8}} }+\frac{{y}^{\mathrm{3}} }{\mathrm{1}−{y}^{\mathrm{8}} }+\frac{{z}^{\mathrm{3}} }{\mathrm{1}−{z}^{\mathrm{8}} } \\ $$
Answered by Subhi last updated on 27/Jun/23

$${put}\:{f}\left({x}\right)\:=\:\frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{8}} } \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{8}} \right)+\mathrm{8}{x}^{\mathrm{7}} \left({x}^{\mathrm{3}} \right)}{\left(\mathrm{1}−{x}^{\mathrm{8}} \right)^{\mathrm{2}} }\:{at}\:{x}\:=\:\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{3}}}\:\left({value}\:{that}\:{achieves}\:{the}\:{equality}\right) \\ $$$${f}^{'} \left(\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{3}}}\right)\:=\:\mathrm{2}.\mathrm{598} \\ $$$${y}_{{f}} −{y}_{\mathrm{0}} \:=\:{m}\left({x}_{{f}} −{x}_{\mathrm{0}} \right) \\ $$$${f}\left({x}\right)\:=\:\mathrm{2}.\mathrm{598}\left({x}−\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{3}}}\right)+\frac{\left(\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{3}}}\right)^{\mathrm{3}} }{\mathrm{1}−\left(\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{\mathrm{3}}}\right)^{\mathrm{8}} } \\ $$$${f}\left({x}\right)\:=\:\mathrm{2}.\mathrm{598}{x}\:−\mathrm{1}.\mathrm{48} \\ $$$${according}\:{to}\:{tangent}\:{theorem} \\ $$$${f}\left({x}\right)+{f}\left({y}\right)+{f}\left({z}\right)\:\geqslant\:\mathrm{2}.\mathrm{589}\left({x}+{y}+{z}\right)−\mathrm{1}.\mathrm{48}×\mathrm{3} \\ $$$$\:=\:\mathrm{2}.\mathrm{589}\left(\frac{\mathrm{3}}{\:^{\mathrm{4}} \sqrt{\mathrm{3}}}\right)−\mathrm{1}.\mathrm{48}×\mathrm{3}\:=\:\mathrm{1}.\mathrm{48}\:{approx}\: \\ $$
Commented by Frix last updated on 28/Jun/23
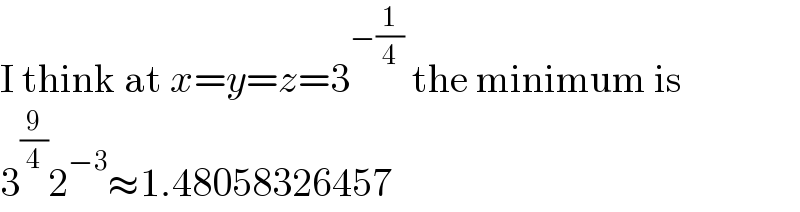
$$\mathrm{I}\:\mathrm{think}\:\mathrm{at}\:{x}={y}={z}=\mathrm{3}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:\mathrm{the}\:\mathrm{minimum}\:\mathrm{is} \\ $$$$\mathrm{3}^{\frac{\mathrm{9}}{\mathrm{4}}} \mathrm{2}^{−\mathrm{3}} \approx\mathrm{1}.\mathrm{48058326457} \\ $$
Commented by York12 last updated on 28/Jun/23

$${thanks}\:{bro} \\ $$
Commented by York12 last updated on 28/Jun/23

$${sir}\:{I}\:{have}\:{sent}\:{you}\:{a}\:{friend}\:{request}\:{on} \\ $$$${discord} \\ $$
Commented by York12 last updated on 28/Jun/23

$$ \\ $$
Commented by York12 last updated on 28/Jun/23
Commented by York12 last updated on 28/Jun/23

$${sir}\:{I}\:{have}\:{sent}\:{you}\:{a}\:{friend}\:{request}\:{on}\: \\ $$$${discord}\:\: \\ $$$${please}\:{accept}\:{sir} \\ $$
