Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7809 by Tawakalitu. last updated on 16/Sep/16

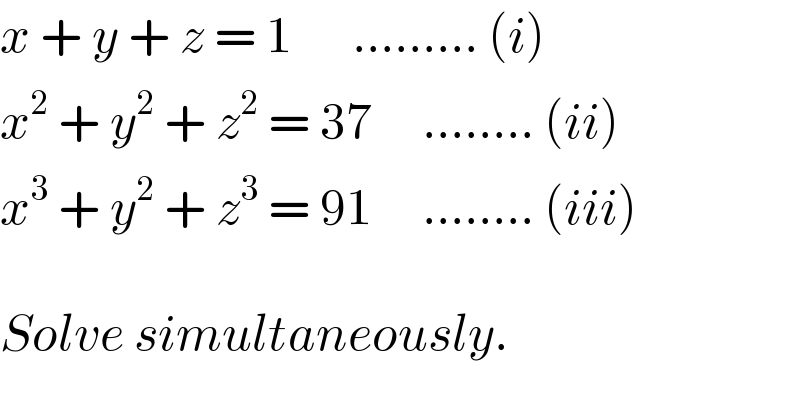
x + y + z = 1 ......... (i) x^2 + y^2 + z^2 = 37 ........ (ii) x^3 + y^2 + z^3 = 91 ........ (iii) Solve simultaneously.

$${x}\:+\:{y}\:+\:{z}\:=\:\mathrm{1}\:\:\:\:\:\:.........\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \:=\:\mathrm{37}\:\:\:\:\:........\:\left({ii}\right) \\ $$$${x}^{\mathrm{3}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{3}} \:=\:\mathrm{91}\:\:\:\:\:........\:\left({iii}\right) \\ $$$$ \\ $$$${Solve}\:{simultaneously}.\: \\ $$

Commented by Tawakalitu. last updated on 16/Sep/16

That is the correct question , no mistake in the last equation ....thanks for your help.

$${That}\:{is}\:{the}\:{correct}\:{question}\:,\:{no}\:{mistake}\:{in}\:{the}\:{last} \\ $$$${equation}\:....{thanks}\:{for}\:{your}\:{help}. \\ $$

Commented by prakash jain last updated on 16/Sep/16

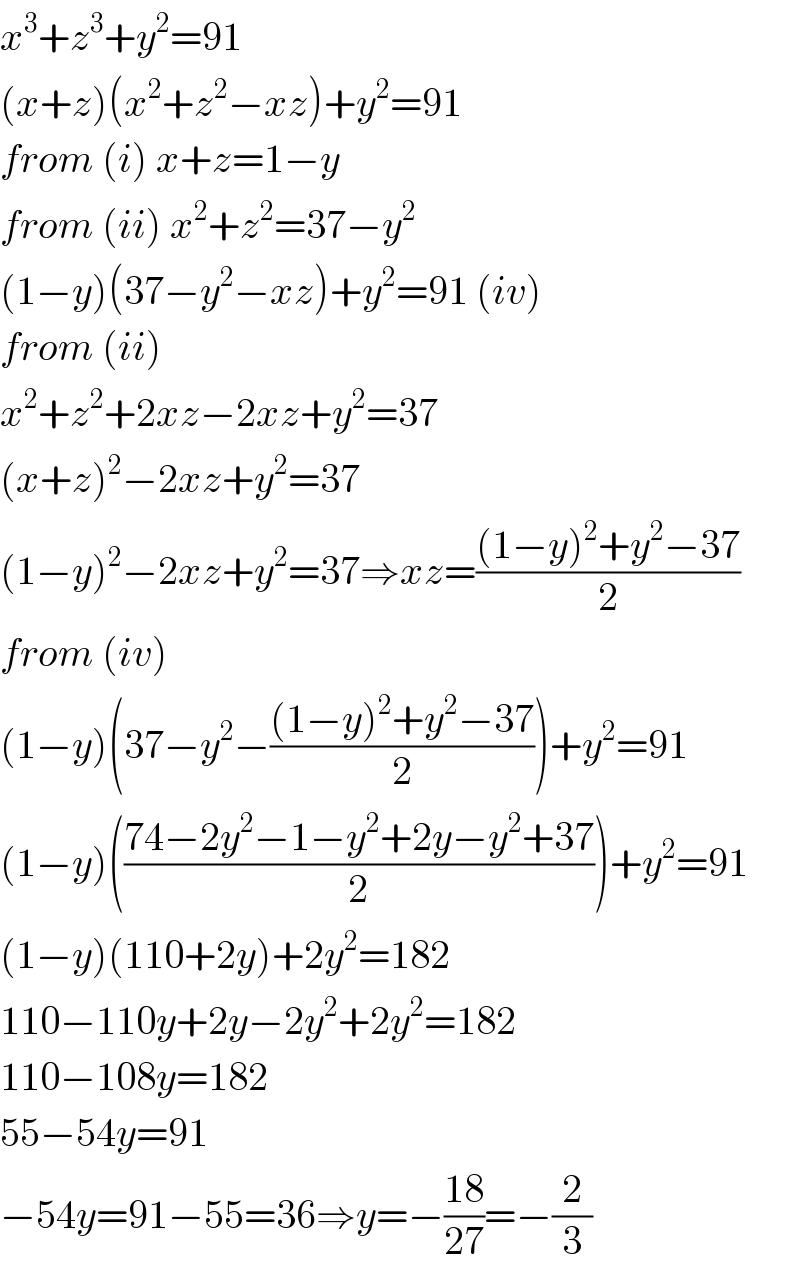
x^3 +z^3 +y^2 =91 (x+z)(x^2 +z^2 −xz)+y^2 =91 from (i) x+z=1−y from (ii) x^2 +z^2 =37−y^2 (1−y)(37−y^2 −xz)+y^2 =91 (iv) from (ii) x^2 +z^2 +2xz−2xz+y^2 =37 (x+z)^2 −2xz+y^2 =37 (1−y)^2 −2xz+y^2 =37⇒xz=(((1−y)^2 +y^2 −37)/2) from (iv) (1−y)(37−y^2 −(((1−y)^2 +y^2 −37)/2))+y^2 =91 (1−y)(((74−2y^2 −1−y^2 +2y−y^2 +37)/2))+y^2 =91 (1−y)(110+2y)+2y^2 =182 110−110y+2y−2y^2 +2y^2 =182 110−108y=182 55−54y=91 −54y=91−55=36⇒y=−((18)/(27))=−(2/3)

$${x}^{\mathrm{3}} +{z}^{\mathrm{3}} +{y}^{\mathrm{2}} =\mathrm{91} \\ $$$$\left({x}+{z}\right)\left({x}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xz}\right)+{y}^{\mathrm{2}} =\mathrm{91} \\ $$$${from}\:\left({i}\right)\:{x}+{z}=\mathrm{1}−{y} \\ $$$${from}\:\left({ii}\right)\:{x}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{37}−{y}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−{y}\right)\left(\mathrm{37}−{y}^{\mathrm{2}} −{xz}\right)+{y}^{\mathrm{2}} =\mathrm{91}\:\left({iv}\right) \\ $$$${from}\:\left({ii}\right) \\ $$$${x}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{xz}−\mathrm{2}{xz}+{y}^{\mathrm{2}} =\mathrm{37} \\ $$$$\left({x}+{z}\right)^{\mathrm{2}} −\mathrm{2}{xz}+{y}^{\mathrm{2}} =\mathrm{37} \\ $$$$\left(\mathrm{1}−{y}\right)^{\mathrm{2}} −\mathrm{2}{xz}+{y}^{\mathrm{2}} =\mathrm{37}\Rightarrow{xz}=\frac{\left(\mathrm{1}−{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{37}}{\mathrm{2}} \\ $$$${from}\:\left({iv}\right) \\ $$$$\left(\mathrm{1}−{y}\right)\left(\mathrm{37}−{y}^{\mathrm{2}} −\frac{\left(\mathrm{1}−{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{37}}{\mathrm{2}}\right)+{y}^{\mathrm{2}} =\mathrm{91} \\ $$$$\left(\mathrm{1}−{y}\right)\left(\frac{\mathrm{74}−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}−{y}^{\mathrm{2}} +\mathrm{2}{y}−{y}^{\mathrm{2}} +\mathrm{37}}{\mathrm{2}}\right)+{y}^{\mathrm{2}} =\mathrm{91} \\ $$$$\left(\mathrm{1}−{y}\right)\left(\mathrm{110}+\mathrm{2}{y}\right)+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{182} \\ $$$$\mathrm{110}−\mathrm{110}{y}+\mathrm{2}{y}−\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} =\mathrm{182} \\ $$$$\mathrm{110}−\mathrm{108}{y}=\mathrm{182} \\ $$$$\mathrm{55}−\mathrm{54}{y}=\mathrm{91} \\ $$$$−\mathrm{54}{y}=\mathrm{91}−\mathrm{55}=\mathrm{36}\Rightarrow{y}=−\frac{\mathrm{18}}{\mathrm{27}}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Commented by prakash jain last updated on 16/Sep/16

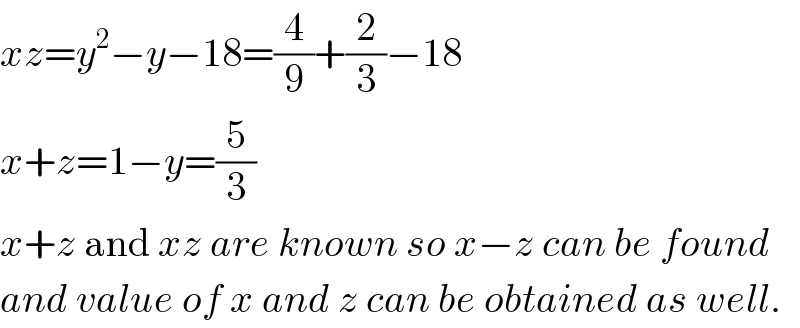
xz=y^2 −y−18=(4/9)+(2/3)−18 x+z=1−y=(5/3) x+z and xz are known so x−z can be found and value of x and z can be obtained as well.

$${xz}={y}^{\mathrm{2}} −{y}−\mathrm{18}=\frac{\mathrm{4}}{\mathrm{9}}+\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{18} \\ $$$${x}+{z}=\mathrm{1}−{y}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${x}+{z}\:\mathrm{and}\:{xz}\:{are}\:{known}\:{so}\:{x}−{z}\:{can}\:{be}\:{found} \\ $$$${and}\:{value}\:{of}\:{x}\:{and}\:{z}\:{can}\:{be}\:{obtained}\:{as}\:{well}. \\ $$

Answered by Rasheed Soomro last updated on 18/Sep/16

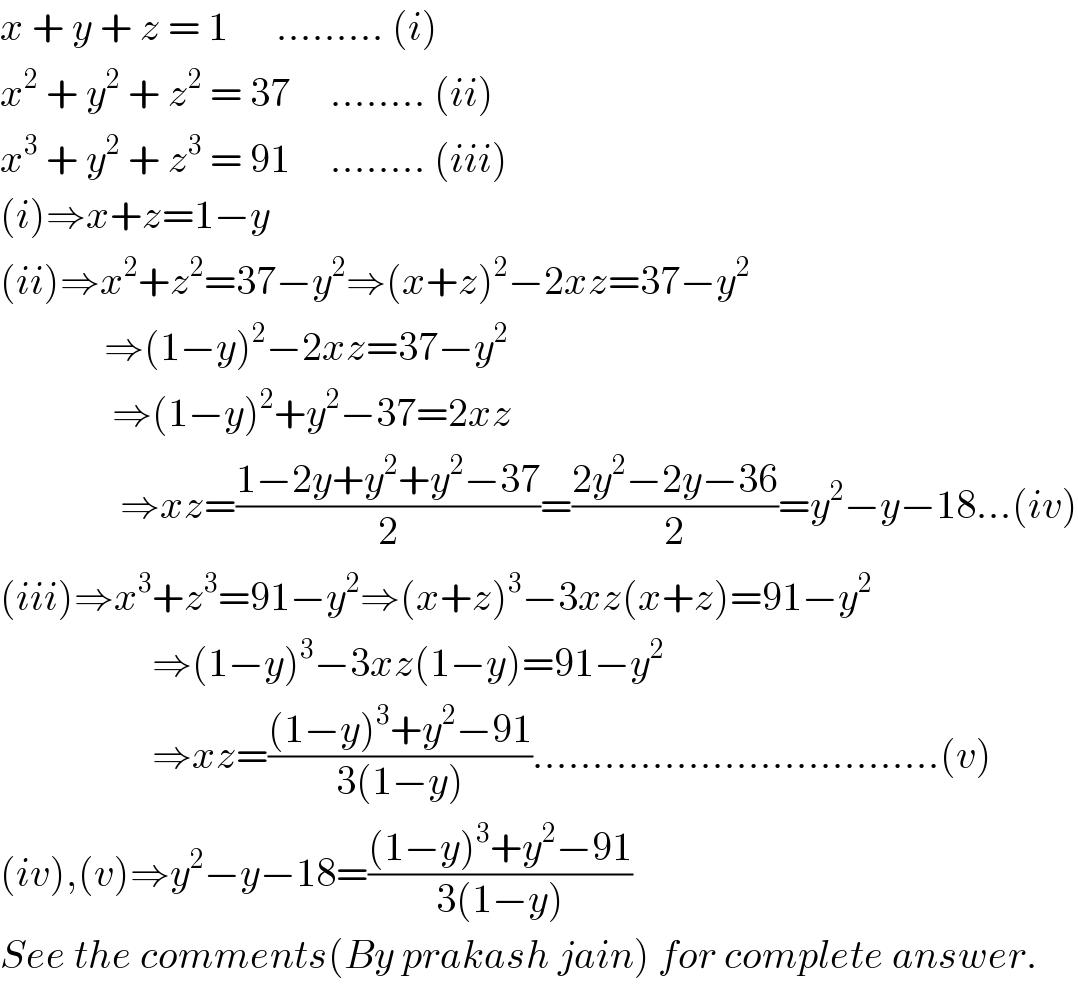
x + y + z = 1 ......... (i) x^2 + y^2 + z^2 = 37 ........ (ii) x^3 + y^2 + z^3 = 91 ........ (iii) (i)⇒x+z=1−y (ii)⇒x^2 +z^2 =37−y^2 ⇒(x+z)^2 −2xz=37−y^2 ⇒(1−y)^2 −2xz=37−y^2 ⇒(1−y)^2 +y^2 −37=2xz ⇒xz=((1−2y+y^2 +y^2 −37)/2)=((2y^2 −2y−36)/2)=y^2 −y−18...(iv) (iii)⇒x^3 +z^3 =91−y^2 ⇒(x+z)^3 −3xz(x+z)=91−y^2 ⇒(1−y)^3 −3xz(1−y)=91−y^2 ⇒xz=(((1−y)^3 +y^2 −91)/(3(1−y)))..................................(v) (iv),(v)⇒y^2 −y−18=(((1−y)^3 +y^2 −91)/(3(1−y))) See the comments(By prakash jain) for complete answer.

$${x}\:+\:{y}\:+\:{z}\:=\:\mathrm{1}\:\:\:\:\:\:.........\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \:=\:\mathrm{37}\:\:\:\:\:........\:\left({ii}\right) \\ $$$${x}^{\mathrm{3}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{3}} \:=\:\mathrm{91}\:\:\:\:\:........\:\left({iii}\right) \\ $$$$\left({i}\right)\Rightarrow{x}+{z}=\mathrm{1}−{y} \\ $$$$\left({ii}\right)\Rightarrow{x}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{37}−{y}^{\mathrm{2}} \Rightarrow\left({x}+{z}\right)^{\mathrm{2}} −\mathrm{2}{xz}=\mathrm{37}−{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left(\mathrm{1}−{y}\right)^{\mathrm{2}} −\mathrm{2}{xz}=\mathrm{37}−{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left(\mathrm{1}−{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{37}=\mathrm{2}{xz} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{xz}=\frac{\mathrm{1}−\mathrm{2}{y}+{y}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{37}}{\mathrm{2}}=\frac{\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}−\mathrm{36}}{\mathrm{2}}={y}^{\mathrm{2}} −{y}−\mathrm{18}...\left({iv}\right) \\ $$$$\left({iii}\right)\Rightarrow{x}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{91}−{y}^{\mathrm{2}} \Rightarrow\left({x}+{z}\right)^{\mathrm{3}} −\mathrm{3}{xz}\left({x}+{z}\right)=\mathrm{91}−{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\left(\mathrm{1}−{y}\right)^{\mathrm{3}} −\mathrm{3}{xz}\left(\mathrm{1}−{y}\right)=\mathrm{91}−{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{xz}=\frac{\left(\mathrm{1}−{y}\right)^{\mathrm{3}} +{y}^{\mathrm{2}} −\mathrm{91}}{\mathrm{3}\left(\mathrm{1}−{y}\right)}..................................\left({v}\right) \\ $$$$\left({iv}\right),\left({v}\right)\Rightarrow{y}^{\mathrm{2}} −{y}−\mathrm{18}=\frac{\left(\mathrm{1}−{y}\right)^{\mathrm{3}} +{y}^{\mathrm{2}} −\mathrm{91}}{\mathrm{3}\left(\mathrm{1}−{y}\right)} \\ $$$${See}\:{the}\:{comments}\left({By}\:{prakash}\:{jain}\right)\:{for}\:{complete}\:{answer}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com