
Question Number 11805 by tawa last updated on 01/Apr/17

$$\mathrm{x}^{\mathrm{y}} \:=\:\mathrm{y}^{\mathrm{x}} \:\:\:\: \\ $$$$\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{y}^{\mathrm{3}} \\ $$$$\mathrm{find}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$
Answered by mrW1 last updated on 01/Apr/17
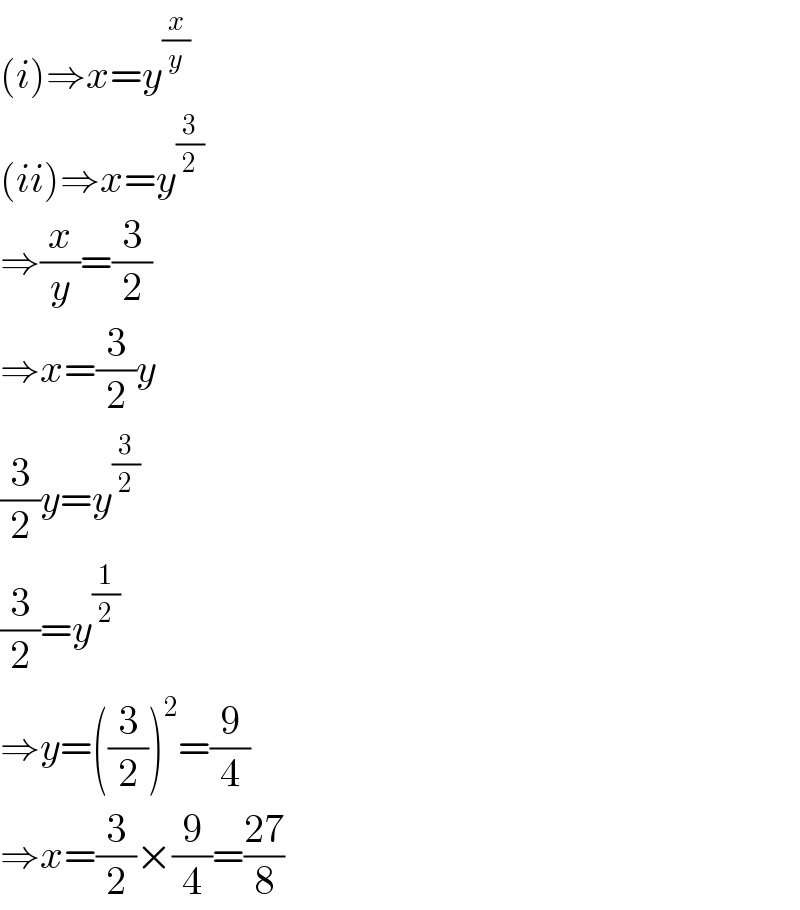
$$\left({i}\right)\Rightarrow{x}={y}^{\frac{{x}}{{y}}} \\ $$$$\left({ii}\right)\Rightarrow{x}={y}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{2}}{y} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{y}={y}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}={y}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow{y}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{9}}{\mathrm{4}}=\frac{\mathrm{27}}{\mathrm{8}} \\ $$
Commented by tawa last updated on 01/Apr/17

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Apr/17
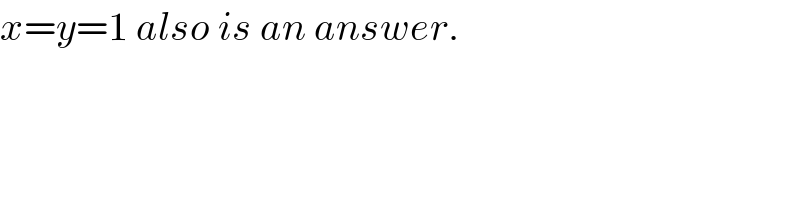
$${x}={y}=\mathrm{1}\:{also}\:{is}\:{an}\:{answer}. \\ $$
Commented by mrW1 last updated on 01/Apr/17

$${that}'{s}\:{right}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/Apr/17
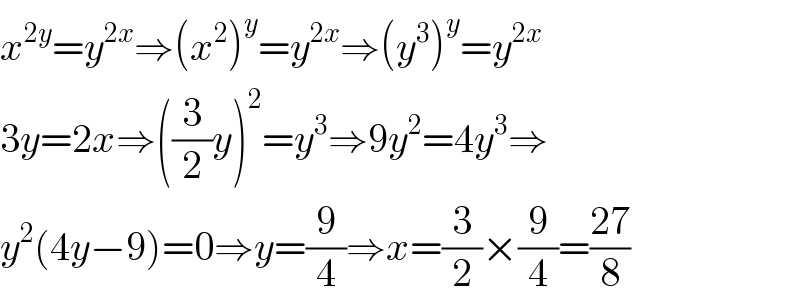
$${x}^{\mathrm{2}{y}} ={y}^{\mathrm{2}{x}} \Rightarrow\left({x}^{\mathrm{2}} \right)^{{y}} ={y}^{\mathrm{2}{x}} \Rightarrow\left({y}^{\mathrm{3}} \right)^{{y}} ={y}^{\mathrm{2}{x}} \\ $$$$\mathrm{3}{y}=\mathrm{2}{x}\Rightarrow\left(\frac{\mathrm{3}}{\mathrm{2}}{y}\right)^{\mathrm{2}} ={y}^{\mathrm{3}} \Rightarrow\mathrm{9}{y}^{\mathrm{2}} =\mathrm{4}{y}^{\mathrm{3}} \Rightarrow \\ $$$${y}^{\mathrm{2}} \left(\mathrm{4}{y}−\mathrm{9}\right)=\mathrm{0}\Rightarrow{y}=\frac{\mathrm{9}}{\mathrm{4}}\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{9}}{\mathrm{4}}=\frac{\mathrm{27}}{\mathrm{8}} \\ $$
