Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 171244 by mathlove last updated on 11/Jun/22

(x/y)+(y/x)=((26)/5) ((x+y)/(x−y))=? (/)

$$\frac{{x}}{{y}}+\frac{{y}}{{x}}=\frac{\mathrm{26}}{\mathrm{5}} \\ $$$$\frac{{x}+{y}}{{x}−{y}}=? \\ $$$$\frac{}{} \\ $$

Commented by infinityaction last updated on 11/Jun/22

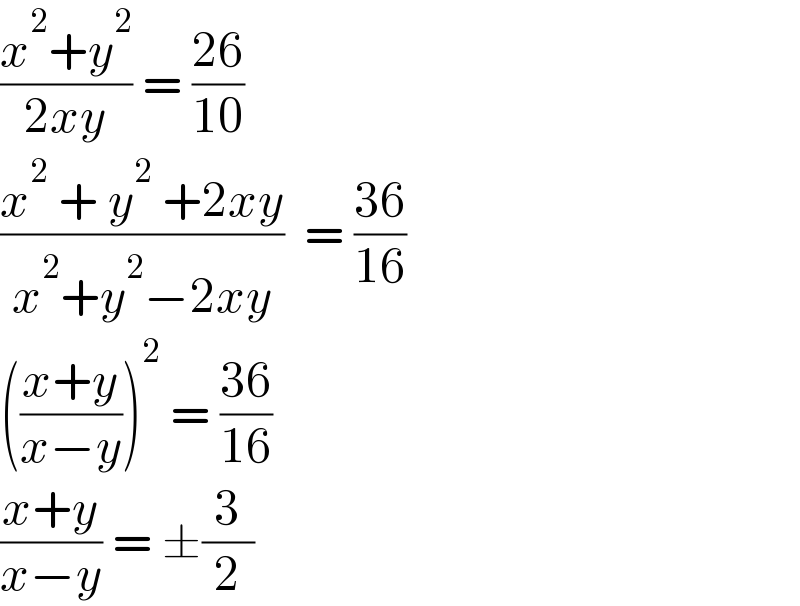
((x^2 +y^2 )/(2xy)) = ((26)/(10)) ((x^2 + y^2 +2xy)/(x^2 +y^2 −2xy)) = ((36)/(16)) (((x+y)/(x−y)))^2 = ((36)/(16)) ((x+y)/(x−y)) = ±(3/2)

$$\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}{xy}}\:=\:\frac{\mathrm{26}}{\mathrm{10}} \\ $$$$\frac{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\mathrm{2}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}}\:\:=\:\frac{\mathrm{36}}{\mathrm{16}} \\ $$$$\left(\frac{{x}+{y}}{{x}−{y}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{36}}{\mathrm{16}} \\ $$$$\frac{{x}+{y}}{{x}−{y}}\:=\:\pm\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 11/Jun/22

GOOD!

$$\mathcal{GOOD}! \\ $$

Commented by udaythool last updated on 11/Jun/22

super

$${super} \\ $$

Answered by Rasheed.Sindhi last updated on 11/Jun/22

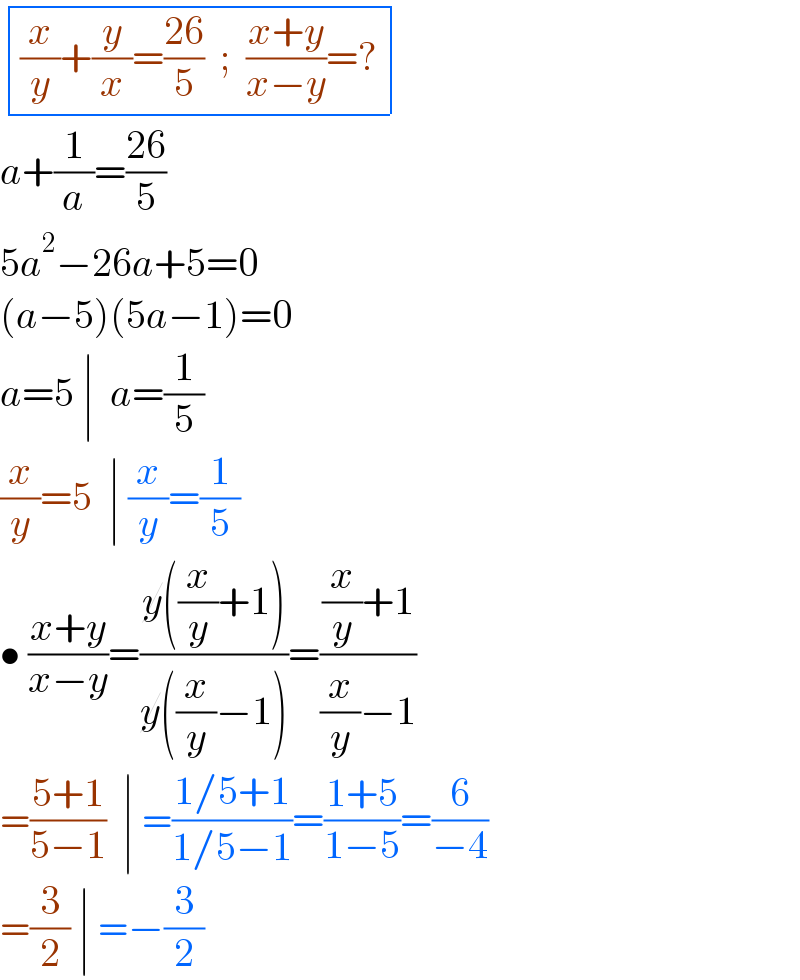
determinant ((((x/y)+(y/x)=((26)/5) ; ((x+y)/(x−y))=?))) a+(1/a)=((26)/5) 5a^2 −26a+5=0 (a−5)(5a−1)=0 a=5 ∣ a=(1/5) (x/y)=5 ∣ (x/y)=(1/5) • ((x+y)/(x−y))=((y((x/y)+1))/(y((x/y)−1)))=(((x/y)+1)/((x/y)−1)) =((5+1)/(5−1)) ∣ =((1/5+1)/(1/5−1))=((1+5)/(1−5))=(6/(−4)) =(3/2) ∣ =−(3/2)

$$\begin{array}{|c|}{\frac{{x}}{{y}}+\frac{{y}}{{x}}=\frac{\mathrm{26}}{\mathrm{5}}\:\:;\:\:\frac{{x}+{y}}{{x}−{y}}=?}\\\hline\end{array} \\ $$$${a}+\frac{\mathrm{1}}{{a}}=\frac{\mathrm{26}}{\mathrm{5}} \\ $$$$\mathrm{5}{a}^{\mathrm{2}} −\mathrm{26}{a}+\mathrm{5}=\mathrm{0} \\ $$$$\left({a}−\mathrm{5}\right)\left(\mathrm{5}{a}−\mathrm{1}\right)=\mathrm{0} \\ $$$${a}=\mathrm{5}\:\mid\:\:{a}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\frac{{x}}{{y}}=\mathrm{5}\:\:\mid\:\frac{{x}}{{y}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\bullet\:\frac{{x}+{y}}{{x}−{y}}=\frac{\cancel{{y}}\left(\frac{{x}}{{y}}+\mathrm{1}\right)}{\cancel{{y}}\left(\frac{{x}}{{y}}−\mathrm{1}\right)}=\frac{\frac{{x}}{{y}}+\mathrm{1}}{\frac{{x}}{{y}}−\mathrm{1}} \\ $$$$=\frac{\mathrm{5}+\mathrm{1}}{\mathrm{5}−\mathrm{1}}\:\:\mid\:=\frac{\mathrm{1}/\mathrm{5}+\mathrm{1}}{\mathrm{1}/\mathrm{5}−\mathrm{1}}=\frac{\mathrm{1}+\mathrm{5}}{\mathrm{1}−\mathrm{5}}=\frac{\mathrm{6}}{−\mathrm{4}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\:\mid\:=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Answered by Rasheed.Sindhi last updated on 11/Jun/22

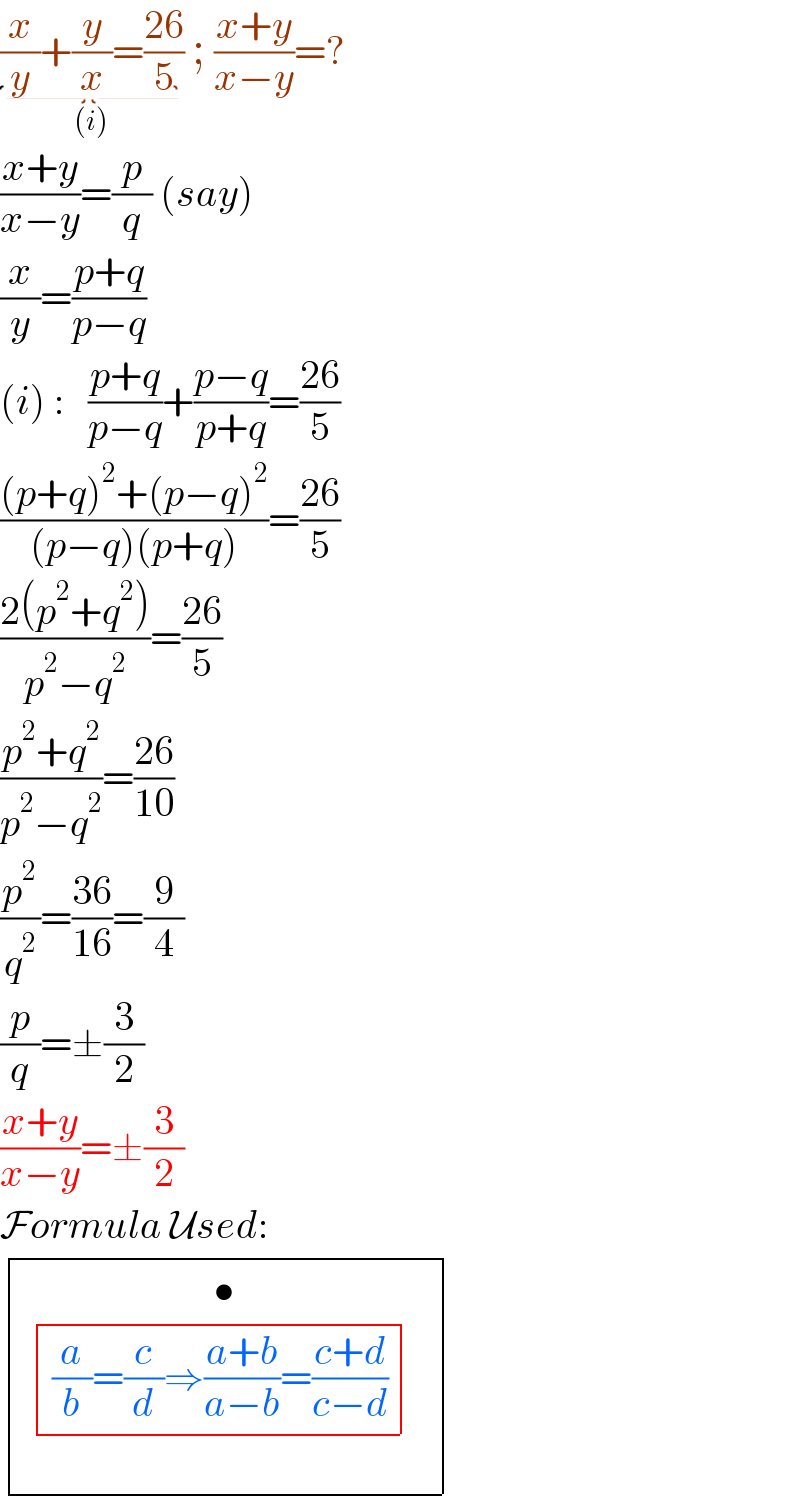
(x/y)+(y/x)=((26)/5)_((i)) ; ((x+y)/(x−y))=? ((x+y)/(x−y))=(p/q) (say) (x/y)=((p+q)/(p−q)) (i) : ((p+q)/(p−q))+((p−q)/(p+q))=((26)/5) (((p+q)^2 +(p−q)^2 )/((p−q)(p+q)))=((26)/5) ((2(p^2 +q^2 ))/(p^2 −q^2 ))=((26)/5) ((p^2 +q^2 )/(p^2 −q^2 ))=((26)/(10)) (p^2 /q^2 )=((36)/(16))=(9/4) (p/q)=±(3/2) ((x+y)/(x−y))=±(3/2) Formula Used: determinant ((( determinant ((((a/b)=(c/d)⇒((a+b)/(a−b))=((c+d)/(c−d)))))_ ^ _() ^(•) )))

$$\underset{\left({i}\right)} {\underbrace{\frac{{x}}{{y}}+\frac{{y}}{{x}}=\frac{\mathrm{26}}{\mathrm{5}}}}\:;\:\frac{{x}+{y}}{{x}−{y}}=?\: \\ $$$$\frac{{x}+{y}}{{x}−{y}}=\frac{{p}}{{q}}\:\left({say}\right) \\ $$$$\frac{{x}}{{y}}=\frac{{p}+{q}}{{p}−{q}} \\ $$$$\left({i}\right)\::\:\:\:\frac{{p}+{q}}{{p}−{q}}+\frac{{p}−{q}}{{p}+{q}}=\frac{\mathrm{26}}{\mathrm{5}} \\ $$$$\frac{\left({p}+{q}\right)^{\mathrm{2}} +\left({p}−{q}\right)^{\mathrm{2}} }{\left({p}−{q}\right)\left({p}+{q}\right)}=\frac{\mathrm{26}}{\mathrm{5}} \\ $$$$\frac{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}{{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }=\frac{\mathrm{26}}{\mathrm{5}} \\ $$$$\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }{{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }=\frac{\mathrm{26}}{\mathrm{10}} \\ $$$$\frac{{p}^{\mathrm{2}} }{{q}^{\mathrm{2}} }=\frac{\mathrm{36}}{\mathrm{16}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\frac{{p}}{{q}}=\pm\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\frac{{x}+{y}}{{x}−{y}}=\pm\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathcal{F}{ormula}\:\mathcal{U}{sed}: \\ $$$$\begin{array}{|c|}{\underset{} {\overset{\bullet} {\:\begin{array}{|c|}{\frac{{a}}{{b}}=\frac{{c}}{{d}}\Rightarrow\frac{{a}+{b}}{{a}−{b}}=\frac{{c}+{d}}{{c}−{d}}}\\\hline\end{array}_{} ^{} }}}\\\hline\end{array} \\ $$

Commented by mathlove last updated on 11/Jun/22

thanks

$${thanks} \\ $$

Commented by haladu last updated on 11/Jun/22

awesome solution

Commented by Rasheed.Sindhi last updated on 11/Jun/22

������

Terms of Service

Privacy Policy

Contact: info@tinkutara.com