
Question Number 195365 by Mr.D.N. last updated on 31/Jul/23

$$\:\: \\ $$$$\:\underset{\mathrm{x}\rightarrow\mathrm{y}} {\overset{\mathrm{lim}} {\:}}\:\frac{\mathrm{tan}\:\mathrm{x}−\mathrm{tany}}{\mathrm{x}−\mathrm{y}} \\ $$$$ \\ $$
Answered by cortano12 last updated on 31/Jul/23
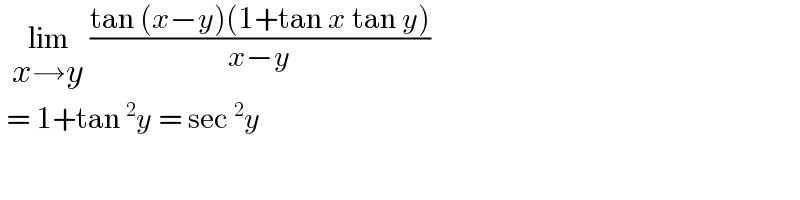
$$\:\:\underset{{x}\rightarrow{y}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left({x}−{y}\right)\left(\mathrm{1}+\mathrm{tan}\:{x}\:\mathrm{tan}\:{y}\right)}{{x}−{y}} \\ $$$$\:=\:\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {y}\:=\:\mathrm{sec}\:^{\mathrm{2}} {y} \\ $$
Answered by kapoorshah last updated on 31/Jul/23
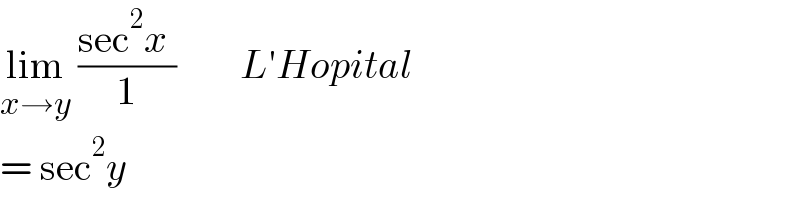
$$\underset{{x}\rightarrow{y}} {\mathrm{lim}}\:\frac{\mathrm{sec}^{\mathrm{2}} {x}\:}{\mathrm{1}}\:\:\:\:\:\:\:\:{L}'{Hopital} \\ $$$$=\:\mathrm{sec}^{\mathrm{2}} {y} \\ $$
