Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 215468 by alephnull last updated on 07/Jan/25

((∂xω)/(∂yω))∙(∂e/∂ω)=? x=f(y) ω=g(y) e=h(ω)

$$\frac{\partial{x}\omega}{\partial{y}\omega}\centerdot\frac{\partial{e}}{\partial\omega}=? \\ $$$${x}={f}\left({y}\right) \\ $$$$\omega={g}\left({y}\right) \\ $$$${e}={h}\left(\omega\right) \\ $$

Answered by MrGaster last updated on 08/Jan/25

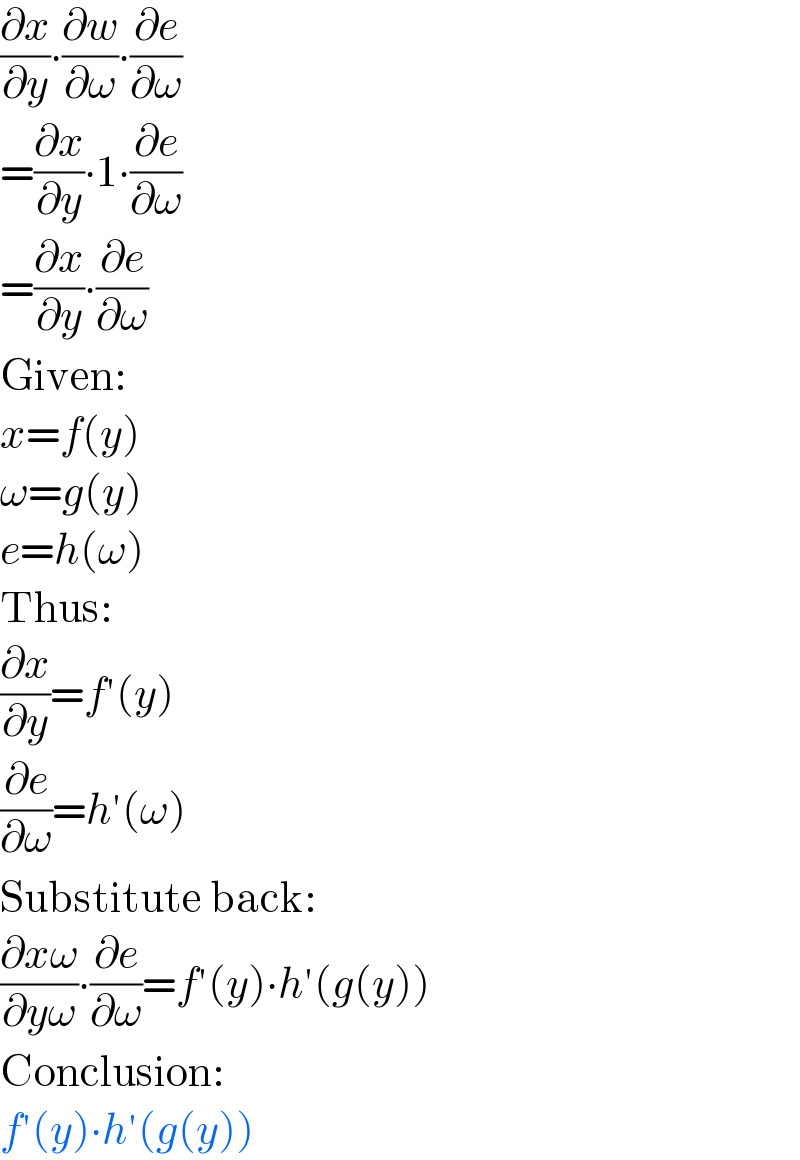
(∂x/∂y)∙(∂w/∂ω)∙(∂e/∂ω) =(∂x/∂y)∙1∙(∂e/∂ω) =(∂x/∂y)∙(∂e/∂ω) Given: x=f(y) ω=g(y) e=h(ω) Thus: (∂x/∂y)=f′(y) (∂e/∂ω)=h′(ω) Substitute back: ((∂xω)/(∂yω))∙(∂e/∂ω)=f′(y)∙h′(g(y)) Conclusion: f′(y)∙h′(g(y))

$$\frac{\partial{x}}{\partial{y}}\centerdot\frac{\partial{w}}{\partial\omega}\centerdot\frac{\partial{e}}{\partial\omega} \\ $$$$=\frac{\partial{x}}{\partial{y}}\centerdot\mathrm{1}\centerdot\frac{\partial{e}}{\partial\omega} \\ $$$$=\frac{\partial{x}}{\partial{y}}\centerdot\frac{\partial{e}}{\partial\omega} \\ $$$$\mathrm{Given}: \\ $$$${x}={f}\left({y}\right) \\ $$$$\omega={g}\left({y}\right) \\ $$$${e}={h}\left(\omega\right) \\ $$$$\mathrm{Thus}: \\ $$$$\frac{\partial{x}}{\partial{y}}={f}'\left({y}\right) \\ $$$$\frac{\partial{e}}{\partial\omega}={h}'\left(\omega\right) \\ $$$$\mathrm{Substitute}\:\mathrm{back}: \\ $$$$\frac{\partial{x}\omega}{\partial{y}\omega}\centerdot\frac{\partial{e}}{\partial\omega}={f}'\left({y}\right)\centerdot{h}'\left({g}\left({y}\right)\right) \\ $$$$\mathrm{Conclusion}: \\ $$$${f}'\left({y}\right)\centerdot{h}'\left({g}\left({y}\right)\right) \\ $$

Commented by alephnull last updated on 08/Jan/25

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by issac last updated on 08/Jan/25

=((ex)/(yω))

$$=\frac{{ex}}{{y}\omega} \\ $$

Commented by MathematicalUser2357 last updated on 29/Mar/25

Did you miscalculated because: (A) you forgot the notation of derivatives (B) you forgot the first principle of derivatives (C) you thinked that as an algebra question

$$\mathrm{Did}\:\mathrm{you}\:\mathrm{miscalculated}\:\mathrm{because}: \\ $$$$\left(\mathrm{A}\right)\:\mathrm{you}\:\mathrm{forgot}\:\mathrm{the}\:\mathrm{notation}\:\mathrm{of}\:\mathrm{derivatives} \\ $$$$\left(\mathrm{B}\right)\:\mathrm{you}\:\mathrm{forgot}\:\mathrm{the}\:\mathrm{first}\:\mathrm{principle}\:\mathrm{of}\:\mathrm{derivatives} \\ $$$$\left(\mathrm{C}\right)\:\mathrm{you}\:\mathrm{thinked}\:\mathrm{that}\:\mathrm{as}\:\mathrm{an}\:\mathrm{algebra}\:\mathrm{question} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com