Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140129 by mathdanisur last updated on 04/May/21

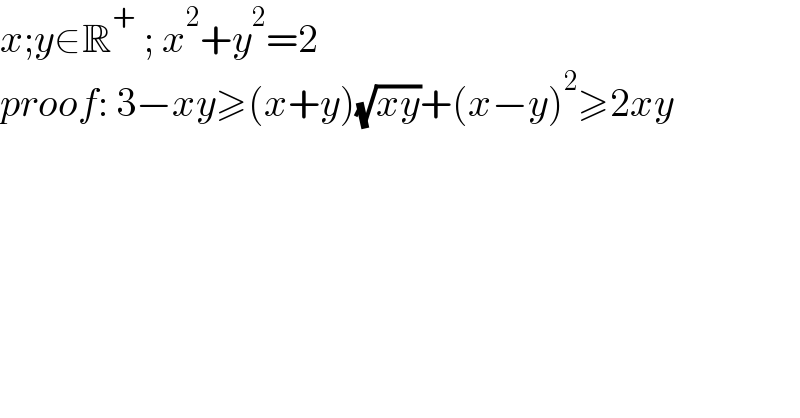
x;y∈R^+ ; x^2 +y^2 =2 proof: 3−xy≥(x+y)(√(xy))+(x−y)^2 ≥2xy

$${x};{y}\in\mathbb{R}^{+} \:;\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2} \\ $$$${proof}:\:\mathrm{3}−{xy}\geqslant\left({x}+{y}\right)\sqrt{{xy}}+\left({x}−{y}\right)^{\mathrm{2}} \geqslant\mathrm{2}{xy} \\ $$

Answered by mr W last updated on 05/May/21

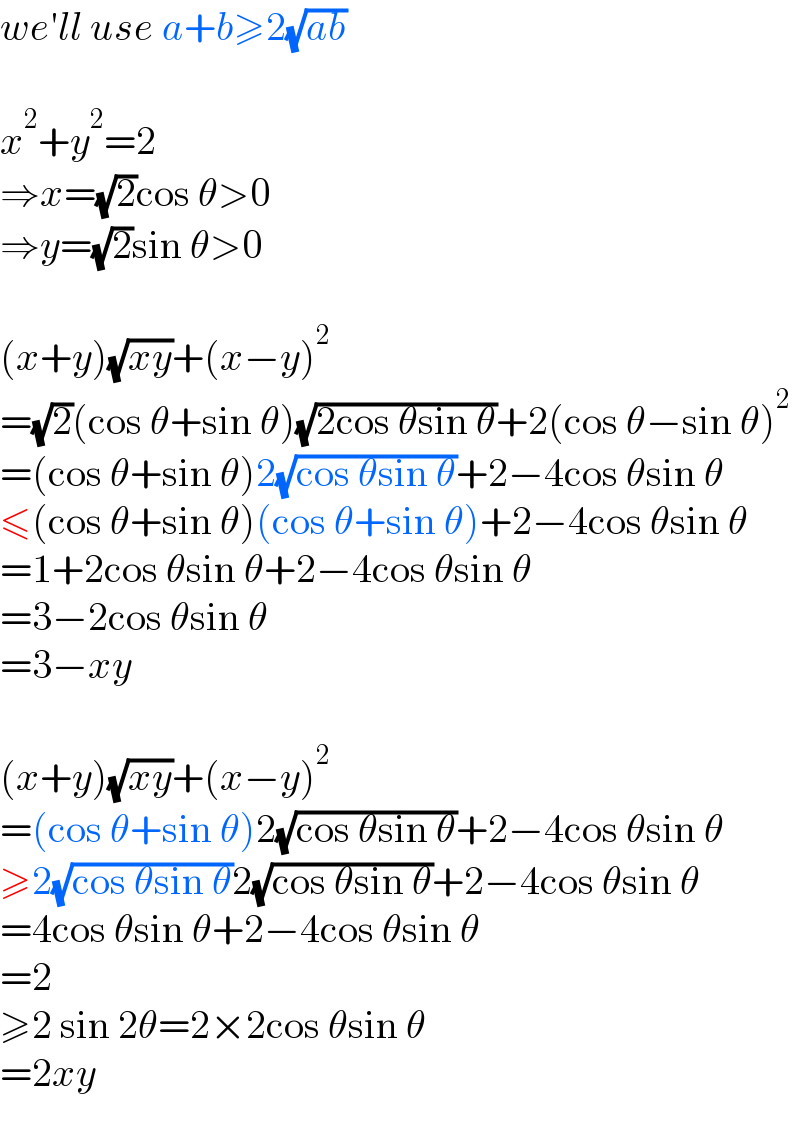
we′ll use a+b≥2(√(ab)) x^2 +y^2 =2 ⇒x=(√2)cos θ>0 ⇒y=(√2)sin θ>0 (x+y)(√(xy))+(x−y)^2 =(√2)(cos θ+sin θ)(√(2cos θsin θ))+2(cos θ−sin θ)^2 =(cos θ+sin θ)2(√(cos θsin θ))+2−4cos θsin θ ≤(cos θ+sin θ)(cos θ+sin θ)+2−4cos θsin θ =1+2cos θsin θ+2−4cos θsin θ =3−2cos θsin θ =3−xy (x+y)(√(xy))+(x−y)^2 =(cos θ+sin θ)2(√(cos θsin θ))+2−4cos θsin θ ≥2(√(cos θsin θ))2(√(cos θsin θ))+2−4cos θsin θ =4cos θsin θ+2−4cos θsin θ =2 ≥2 sin 2θ=2×2cos θsin θ =2xy

$${we}'{ll}\:{use}\:{a}+{b}\geqslant\mathrm{2}\sqrt{{ab}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{2}}\mathrm{cos}\:\theta>\mathrm{0} \\ $$$$\Rightarrow{y}=\sqrt{\mathrm{2}}\mathrm{sin}\:\theta>\mathrm{0} \\ $$$$ \\ $$$$\left({x}+{y}\right)\sqrt{{xy}}+\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$=\sqrt{\mathrm{2}}\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)\sqrt{\mathrm{2cos}\:\theta\mathrm{sin}\:\theta}+\mathrm{2}\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)\mathrm{2}\sqrt{\mathrm{cos}\:\theta\mathrm{sin}\:\theta}+\mathrm{2}−\mathrm{4cos}\:\theta\mathrm{sin}\:\theta \\ $$$$\leqslant\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)+\mathrm{2}−\mathrm{4cos}\:\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{1}+\mathrm{2cos}\:\theta\mathrm{sin}\:\theta+\mathrm{2}−\mathrm{4cos}\:\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{3}−\mathrm{2cos}\:\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{3}−{xy} \\ $$$$ \\ $$$$\left({x}+{y}\right)\sqrt{{xy}}+\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)\mathrm{2}\sqrt{\mathrm{cos}\:\theta\mathrm{sin}\:\theta}+\mathrm{2}−\mathrm{4cos}\:\theta\mathrm{sin}\:\theta \\ $$$$\geqslant\mathrm{2}\sqrt{\mathrm{cos}\:\theta\mathrm{sin}\:\theta}\mathrm{2}\sqrt{\mathrm{cos}\:\theta\mathrm{sin}\:\theta}+\mathrm{2}−\mathrm{4cos}\:\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{4cos}\:\theta\mathrm{sin}\:\theta+\mathrm{2}−\mathrm{4cos}\:\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{2} \\ $$$$\geqslant\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2}×\mathrm{2cos}\:\theta\mathrm{sin}\:\theta \\ $$$$=\mathrm{2}{xy} \\ $$

Commented by mathdanisur last updated on 05/May/21

cool thankyou sir

$${cool}\:{thankyou}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com