Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 197475 by mnjuly1970 last updated on 19/Sep/23

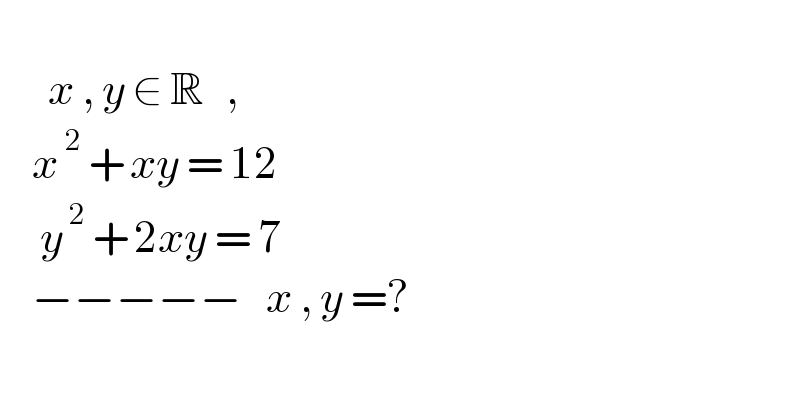
x , y ∈ R , x^( 2) + xy = 12 y^( 2) + 2xy = 7 −−−−− x , y =?

$$ \\ $$$$\:\:\:\:\:\:{x}\:,\:{y}\:\in\:\mathbb{R}\:\:\:, \\ $$$$\:\:\:\:{x}^{\:\mathrm{2}} \:+\:{xy}\:=\:\mathrm{12} \\ $$$$\:\:\:\:\:{y}^{\:\mathrm{2}} \:+\:\mathrm{2}{xy}\:=\:\mathrm{7}\: \\ $$$$\:\:\:\:−−−−−\:\:\:{x}\:,\:{y}\:=? \\ $$

Answered by Sutrisno last updated on 19/Sep/23

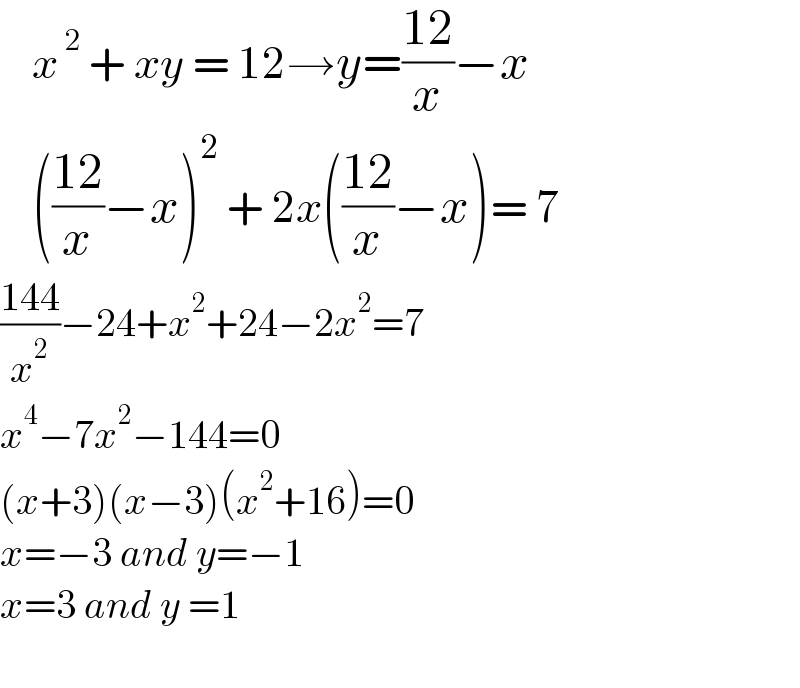
x^( 2) + xy = 12→y=((12)/x)−x (((12)/x)−x)^2 + 2x(((12)/x)−x)= 7 ((144)/x^2 )−24+x^2 +24−2x^2 =7 x^4 −7x^2 −144=0 (x+3)(x−3)(x^2 +16)=0 x=−3 and y=−1 x=3 and y =1

$$\:\:\:\:{x}^{\:\mathrm{2}} \:+\:{xy}\:=\:\mathrm{12}\rightarrow{y}=\frac{\mathrm{12}}{{x}}−{x} \\ $$$$\:\:\:\:\left(\frac{\mathrm{12}}{{x}}−{x}\right)^{\mathrm{2}} \:+\:\mathrm{2}{x}\left(\frac{\mathrm{12}}{{x}}−{x}\right)=\:\mathrm{7}\: \\ $$$$\frac{\mathrm{144}}{{x}^{\mathrm{2}} }−\mathrm{24}+{x}^{\mathrm{2}} +\mathrm{24}−\mathrm{2}{x}^{\mathrm{2}} =\mathrm{7} \\ $$$${x}^{\mathrm{4}} −\mathrm{7}{x}^{\mathrm{2}} −\mathrm{144}=\mathrm{0} \\ $$$$\left({x}+\mathrm{3}\right)\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{16}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{3}\:{and}\:{y}=−\mathrm{1} \\ $$$${x}=\mathrm{3}\:{and}\:{y}\:=\mathrm{1} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 19/Sep/23

thx alot sir

$${thx}\:{alot}\:{sir} \\ $$

Answered by Frix last updated on 19/Sep/23

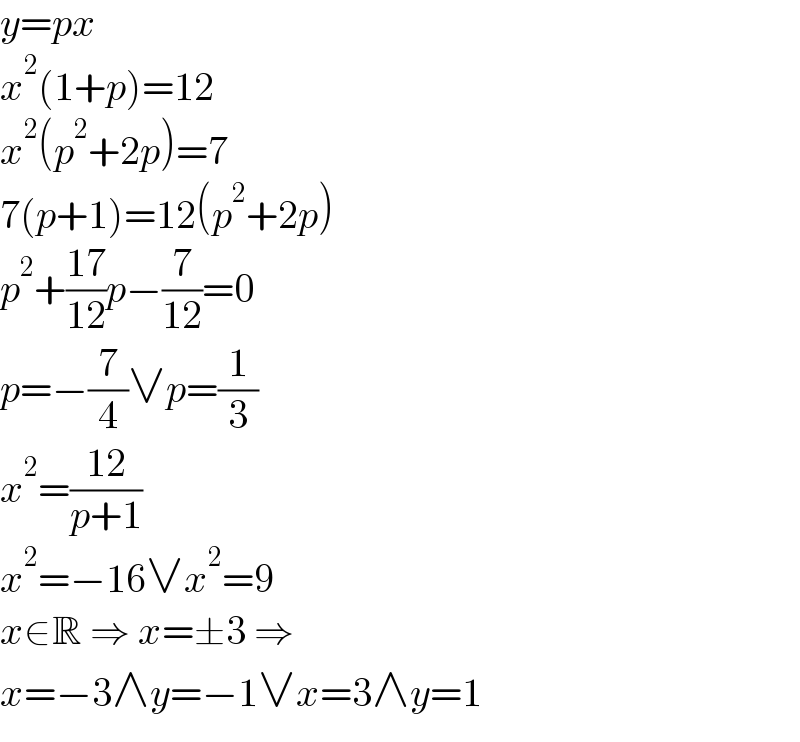
y=px x^2 (1+p)=12 x^2 (p^2 +2p)=7 7(p+1)=12(p^2 +2p) p^2 +((17)/(12))p−(7/(12))=0 p=−(7/4)∨p=(1/3) x^2 =((12)/(p+1)) x^2 =−16∨x^2 =9 x∈R ⇒ x=±3 ⇒ x=−3∧y=−1∨x=3∧y=1

$${y}={px} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{1}+{p}\right)=\mathrm{12} \\ $$$${x}^{\mathrm{2}} \left({p}^{\mathrm{2}} +\mathrm{2}{p}\right)=\mathrm{7} \\ $$$$\mathrm{7}\left({p}+\mathrm{1}\right)=\mathrm{12}\left({p}^{\mathrm{2}} +\mathrm{2}{p}\right) \\ $$$${p}^{\mathrm{2}} +\frac{\mathrm{17}}{\mathrm{12}}{p}−\frac{\mathrm{7}}{\mathrm{12}}=\mathrm{0} \\ $$$${p}=−\frac{\mathrm{7}}{\mathrm{4}}\vee{p}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{12}}{{p}+\mathrm{1}} \\ $$$${x}^{\mathrm{2}} =−\mathrm{16}\vee{x}^{\mathrm{2}} =\mathrm{9} \\ $$$${x}\in\mathbb{R}\:\Rightarrow\:{x}=\pm\mathrm{3}\:\Rightarrow \\ $$$${x}=−\mathrm{3}\wedge{y}=−\mathrm{1}\vee{x}=\mathrm{3}\wedge{y}=\mathrm{1} \\ $$

Answered by Rasheed.Sindhi last updated on 21/Sep/23

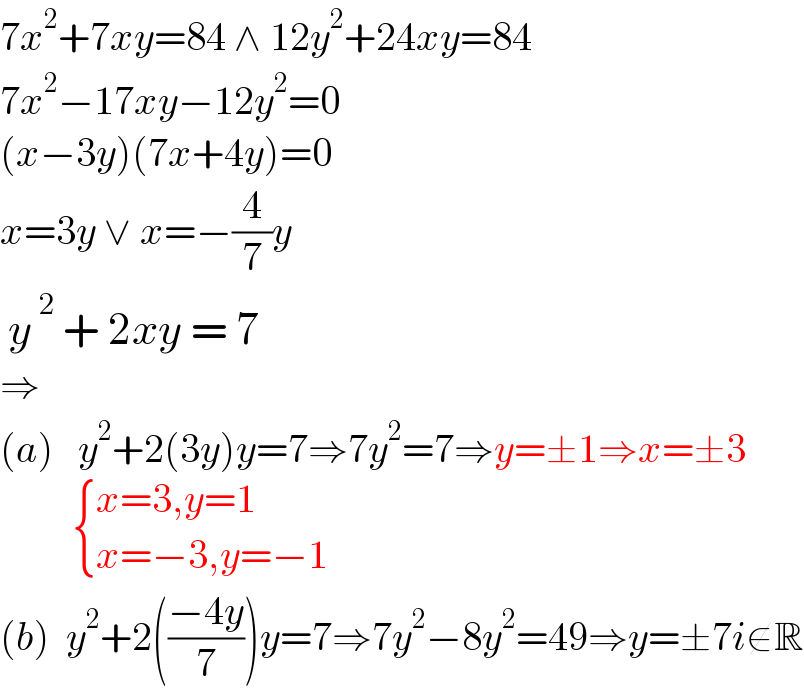
7x^2 +7xy=84 ∧ 12y^2 +24xy=84 7x^2 −17xy−12y^2 =0 (x−3y)(7x+4y)=0 x=3y ∨ x=−(4/7)y y^( 2) + 2xy = 7 ⇒ (a) y^2 +2(3y)y=7⇒7y^2 =7⇒y=±1⇒x=±3 { ((x=3,y=1)),((x=−3,y=−1)) :} (b) y^2 +2(((−4y)/7))y=7⇒7y^2 −8y^2 =49⇒y=±7i∉R

$$\mathrm{7}{x}^{\mathrm{2}} +\mathrm{7}{xy}=\mathrm{84}\:\wedge\:\mathrm{12}{y}^{\mathrm{2}} +\mathrm{24}{xy}=\mathrm{84} \\ $$$$\mathrm{7}{x}^{\mathrm{2}} −\mathrm{17}{xy}−\mathrm{12}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}−\mathrm{3}{y}\right)\left(\mathrm{7}{x}+\mathrm{4}{y}\right)=\mathrm{0} \\ $$$${x}=\mathrm{3}{y}\:\vee\:{x}=−\frac{\mathrm{4}}{\mathrm{7}}{y} \\ $$$$\:{y}^{\:\mathrm{2}} \:+\:\mathrm{2}{xy}\:=\:\mathrm{7} \\ $$$$\Rightarrow \\ $$$$\left({a}\right)\:\:\:{y}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}{y}\right){y}=\mathrm{7}\Rightarrow\mathrm{7}{y}^{\mathrm{2}} =\mathrm{7}\Rightarrow{y}=\pm\mathrm{1}\Rightarrow{x}=\pm\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\begin{cases}{{x}=\mathrm{3},{y}=\mathrm{1}}\\{{x}=−\mathrm{3},{y}=−\mathrm{1}}\end{cases} \\ $$$$\left({b}\right)\:\:{y}^{\mathrm{2}} +\mathrm{2}\left(\frac{−\mathrm{4}{y}}{\mathrm{7}}\right){y}=\mathrm{7}\Rightarrow\mathrm{7}{y}^{\mathrm{2}} −\mathrm{8}{y}^{\mathrm{2}} =\mathrm{49}\Rightarrow{y}=\pm\mathrm{7}{i}\notin\mathbb{R} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com