Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 130149 by liberty last updated on 22/Jan/21

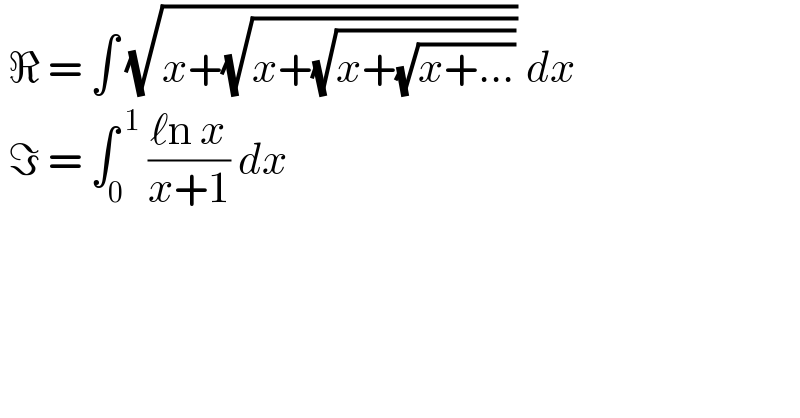
ℜ = ∫ (√(x+(√(x+(√(x+(√(x+...)))))))) dx ℑ = ∫_0 ^( 1) ((ℓn x)/(x+1)) dx

$$\:\Re\:=\:\int\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}}\:{dx} \\ $$$$\:\Im\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\ell\mathrm{n}\:{x}}{{x}+\mathrm{1}}\:{dx}\: \\ $$

Answered by MJS_new last updated on 22/Jan/21

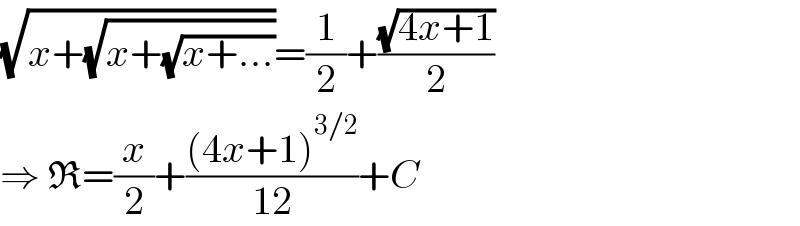
(√(x+(√(x+(√(x+...))))))=(1/2)+((√(4x+1))/2) ⇒ R=(x/2)+(((4x+1)^(3/2) )/(12))+C

$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{4}{x}+\mathrm{1}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathfrak{R}=\frac{{x}}{\mathrm{2}}+\frac{\left(\mathrm{4}{x}+\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{12}}+{C} \\ $$

Commented by liberty last updated on 22/Jan/21

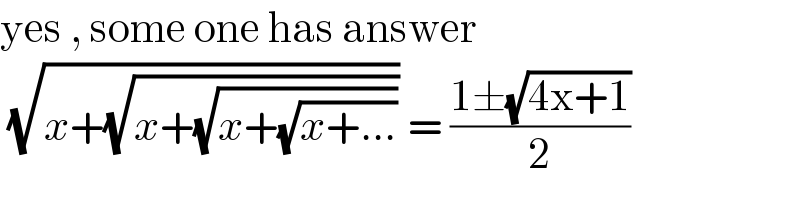
yes , some one has answer (√(x+(√(x+(√(x+(√(x+...)))))))) = ((1±(√(4x+1)))/2)

$$\mathrm{yes}\:,\:\mathrm{some}\:\mathrm{one}\:\mathrm{has}\:\mathrm{answer}\: \\ $$$$\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}}\:=\:\frac{\mathrm{1}\pm\sqrt{\mathrm{4x}+\mathrm{1}}}{\mathrm{2}} \\ $$

Commented by MJS_new last updated on 23/Jan/21

y=(√(x+(√(x+(√(x+...)))))) both sides ≥0 y^2 =x+(√(x+(√(x+(√(x+...)))))) y^2 =x+y this has 2 solutions but only the “+” is right. try with any x to see

$${y}=\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}} \\ $$$$\mathrm{both}\:\mathrm{sides}\:\geqslant\mathrm{0} \\ $$$${y}^{\mathrm{2}} ={x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}} \\ $$$${y}^{\mathrm{2}} ={x}+{y} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{2}\:\mathrm{solutions}\:\mathrm{but}\:\mathrm{only}\:\mathrm{the}\:``+''\:\mathrm{is}\:\mathrm{right}. \\ $$$$\mathrm{try}\:\mathrm{with}\:\mathrm{any}\:{x}\:\mathrm{to}\:\mathrm{see} \\ $$

Commented by liberty last updated on 23/Jan/21

yes...correct

$$\mathrm{yes}...\mathrm{correct} \\ $$

Answered by Lordose last updated on 23/Jan/21

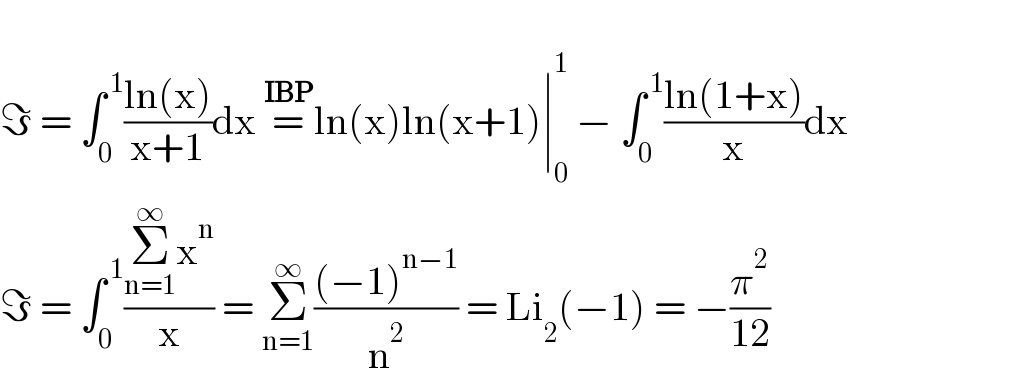
ℑ = ∫_0 ^( 1) ((ln(x))/(x+1))dx =^(IBP) ln(x)ln(x+1)∣_0 ^1 − ∫_0 ^( 1) ((ln(1+x))/x)dx ℑ = ∫_0 ^( 1) ((Σ_(n=1) ^∞ x^n )/x) = Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) = Li_2 (−1) = −(π^2 /(12))

$$ \\ $$$$\Im\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\overset{\boldsymbol{\mathrm{IBP}}} {=}\mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\Im\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}} }{\mathrm{x}}\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\:=\:\mathrm{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)\:=\:−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by benjo_mathlover last updated on 23/Jan/21

−(π^2 /(12))

$$−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Answered by benjo_mathlover last updated on 23/Jan/21

ℑ= ∫_0 ^( 1) ((ln x)/(x+1)) dx = ∫_0 ^( 1) ln x (Σ_(k=0) ^∞ (−1)^k x^k ) dx = Σ_(k=0) ^∞ (−1)^k ∫_0 ^( 1) x^k ln x dx = Σ_(k=0) ^∞ (−1)^k [(x^(k+1) /(k+1)) ln x−(x^(k+1) /((k+1)^2 ))]_0 ^1 = Σ_(k=0) ^∞ (−1)^k (1/((k+1)^2 )) = −Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) = −[Σ_(n=1) ^∞ (1/n^2 )−Σ_(n=1) ^∞ (2/((2n)^2 )) ] = −(1−(1/2))Σ_(n=1) ^∞ (1/n^2 ) = −(1/2).(π^2 /6)= −(π^2 /(12))

$$\Im=\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{x}+\mathrm{1}}\:\mathrm{dx}\:=\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{ln}\:\mathrm{x}\:\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \right)\:\mathrm{dx} \\ $$$$=\:\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{k}} \:\mathrm{ln}\:\mathrm{x}\:\mathrm{dx}\: \\ $$$$=\:\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\left[\frac{\mathrm{x}^{\mathrm{k}+\mathrm{1}} }{\mathrm{k}+\mathrm{1}}\:\mathrm{ln}\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{k}+\mathrm{1}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\:−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=\:\:−\left[\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\left(\mathrm{2n}\right)^{\mathrm{2}} }\:\right]\: \\ $$$$=\:\:−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\:\:−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\:\:−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com