
Question Number 145256 by Gbenga last updated on 03/Jul/21

$${x}^{{x}^{{x}} } =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\sqrt{\mathrm{2}}} \\ $$$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{x}} \\ $$
Commented by justtry last updated on 04/Jul/21
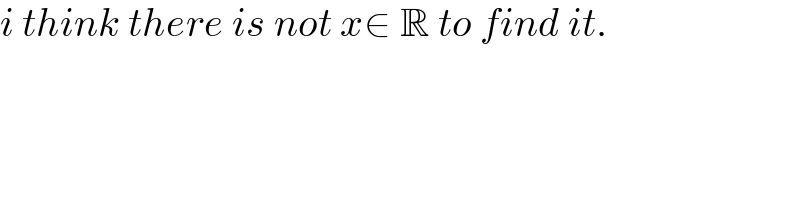
$${i}\:{think}\:{there}\:{is}\:{not}\:{x}\in\:\mathbb{R}\:{to}\:{find}\:{it}. \\ $$$$ \\ $$
Answered by mr W last updated on 04/Jul/21
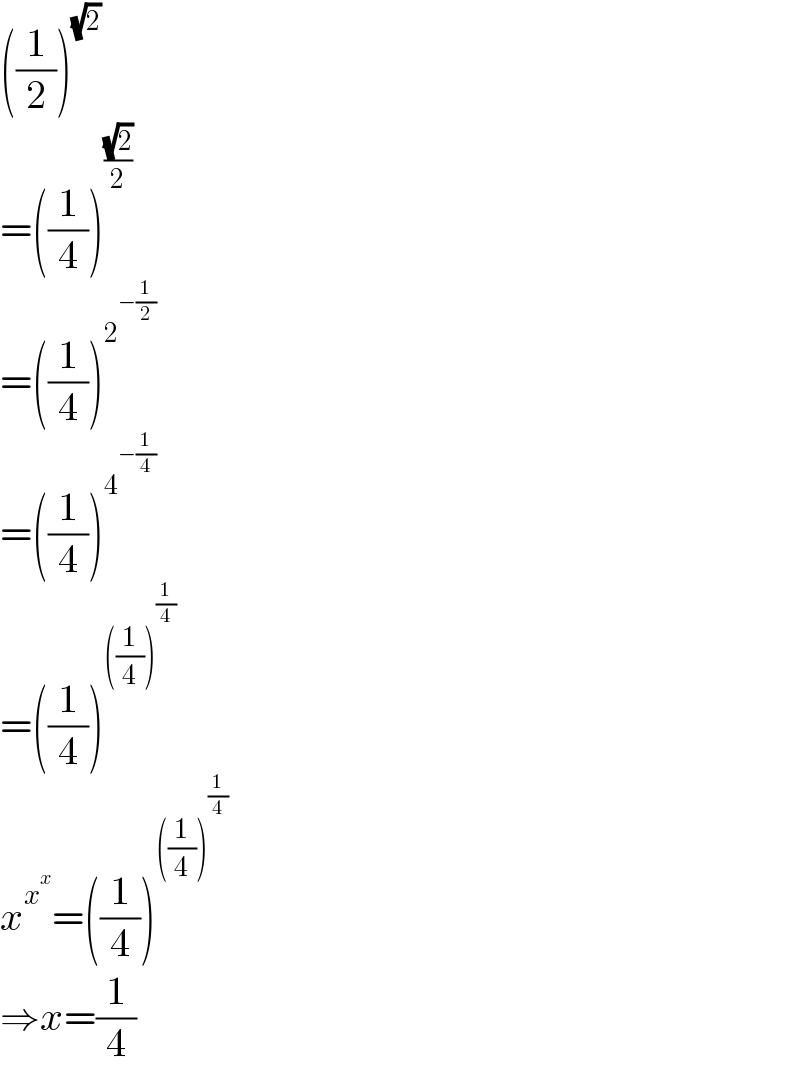
$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\sqrt{\mathrm{2}}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{4}^{−\frac{\mathrm{1}}{\mathrm{4}}} } \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} } \\ $$$${x}^{{x}^{{x}} } =\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} } \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
