Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 183989 by HeferH last updated on 01/Jan/23

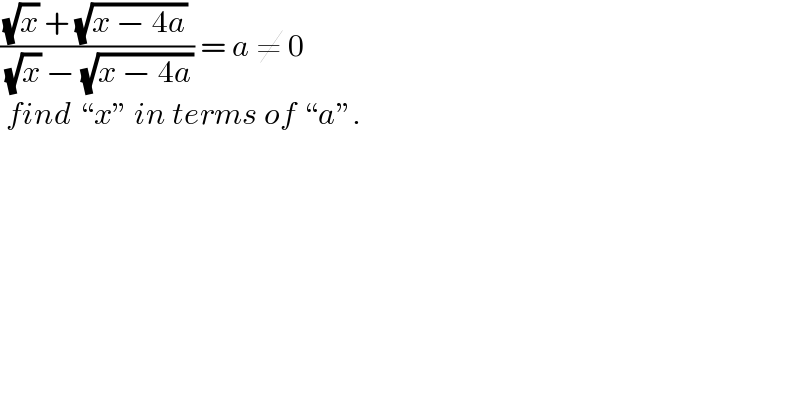
(((√x) + (√(x − 4a)))/( (√x) − (√(x − 4a)))) = a ≠ 0 find “x” in terms of “a”.

$$\frac{\sqrt{{x}}\:+\:\sqrt{{x}\:−\:\mathrm{4}{a}}}{\:\sqrt{{x}}\:−\:\sqrt{{x}\:−\:\mathrm{4}{a}}}\:=\:{a}\:\neq\:\mathrm{0} \\ $$$$\:{find}\:``{x}''\:{in}\:{terms}\:{of}\:``{a}''.\: \\ $$

Commented by Frix last updated on 01/Jan/23

I get x=(a+1)^2

$$\mathrm{I}\:\mathrm{get}\:{x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \\ $$

Answered by Rasheed.Sindhi last updated on 01/Jan/23

(((√x) + (√(x − 4a)))/( (√x) − (√(x − 4a)))) = a ≠ 0 find “x” in terms of “a”. (((√x) +(√(x−4a)) )/( (√x) −(√(x−4a)) ))+1=a+1 ((2(√x))/( (√x) −(√(x−4a)) ))=a+1 2(√x) =a(√x) −a(√(x−4a)) +(√x) −(√(x−4a)) a(√x) −(√x) =a(√(x−4a)) +(√(x−4a)) (√x) (a−1)=(√(x−4a)) (a+1) (((√(x−4a)) )/( (√x)))=((a−1)/(a+1)) ((x−4a)/x)=(((a−1)/(a+1)))^2 1−((4a)/x)=((a^2 −2a+1)/(a^2 +2a+1)) −((4a)/x)=((a^2 −2a+1)/(a^2 +2a+1))−1=((−4a)/((a+1)^2 )) (1/x)=(1/((a+1)^2 )) [∵ a≠0] x=(a+1)^2

$$\frac{\sqrt{{x}}\:+\:\sqrt{{x}\:−\:\mathrm{4}{a}}}{\:\sqrt{{x}}\:−\:\sqrt{{x}\:−\:\mathrm{4}{a}}}\:=\:{a}\:\neq\:\mathrm{0} \\ $$$$\:{find}\:``{x}''\:{in}\:{terms}\:{of}\:``{a}''.\: \\ $$$$\frac{\sqrt{{x}}\:+\sqrt{{x}−\mathrm{4}{a}}\:}{\:\sqrt{{x}}\:−\sqrt{{x}−\mathrm{4}{a}}\:}+\mathrm{1}={a}+\mathrm{1} \\ $$$$\frac{\mathrm{2}\sqrt{{x}}}{\:\sqrt{{x}}\:−\sqrt{{x}−\mathrm{4}{a}}\:}={a}+\mathrm{1} \\ $$$$\mathrm{2}\sqrt{{x}}\:={a}\sqrt{{x}}\:−{a}\sqrt{{x}−\mathrm{4}{a}}\:+\sqrt{{x}}\:−\sqrt{{x}−\mathrm{4}{a}}\: \\ $$$${a}\sqrt{{x}}\:−\sqrt{{x}}\:={a}\sqrt{{x}−\mathrm{4}{a}}\:+\sqrt{{x}−\mathrm{4}{a}}\: \\ $$$$\sqrt{{x}}\:\left({a}−\mathrm{1}\right)=\sqrt{{x}−\mathrm{4}{a}}\:\left({a}+\mathrm{1}\right) \\ $$$$\frac{\sqrt{{x}−\mathrm{4}{a}}\:}{\:\sqrt{{x}}}=\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\frac{{x}−\mathrm{4}{a}}{{x}}=\left(\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}−\frac{\mathrm{4}{a}}{{x}}=\frac{{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}} \\ $$$$−\frac{\mathrm{4}{a}}{{x}}=\frac{{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}}−\mathrm{1}=\frac{−\mathrm{4}{a}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\:\:\:\left[\because\:{a}\neq\mathrm{0}\right] \\ $$$${x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \\ $$

Answered by a.lgnaoui last updated on 01/Jan/23

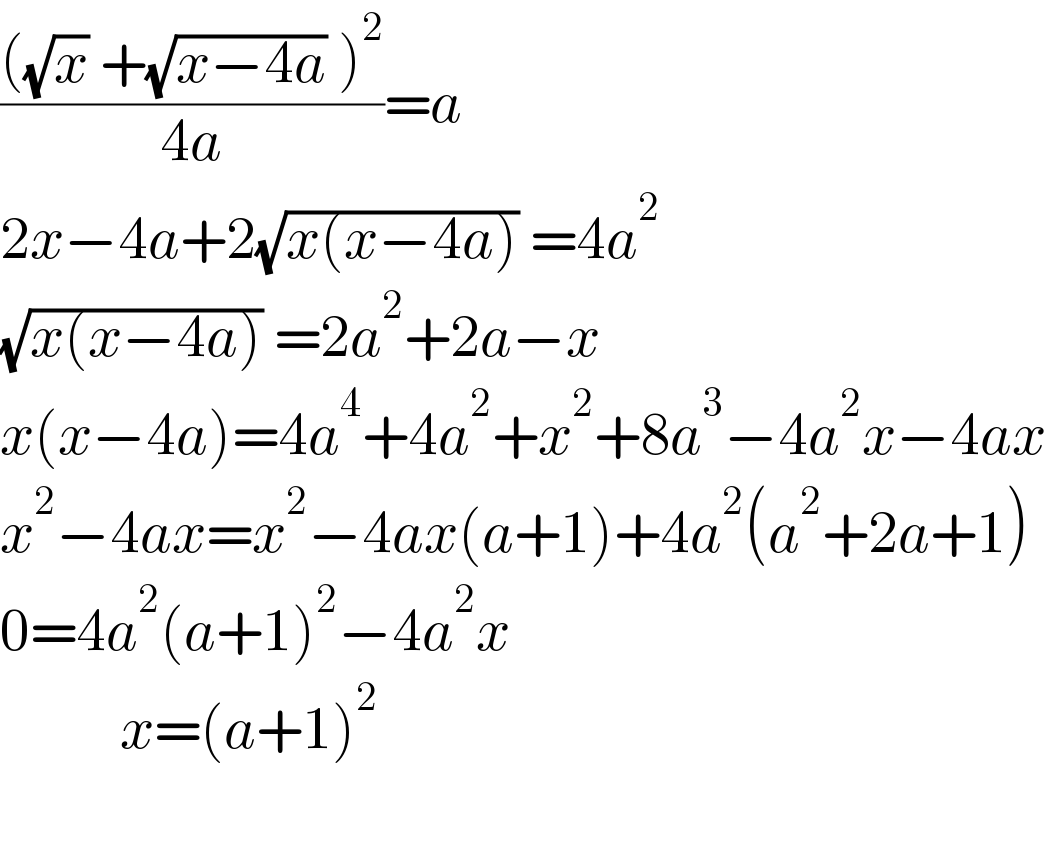
((((√x) +(√(x−4a)) )^2 )/(4a))=a 2x−4a+2(√(x(x−4a))) =4a^2 (√(x(x−4a))) =2a^2 +2a−x x(x−4a)=4a^4 +4a^2 +x^2 +8a^3 −4a^2 x−4ax x^2 −4ax=x^2 −4ax(a+1)+4a^2 (a^2 +2a+1) 0=4a^2 (a+1)^2 −4a^2 x x=(a+1)^2

$$\frac{\left(\sqrt{{x}}\:+\sqrt{{x}−\mathrm{4}{a}}\:\right)^{\mathrm{2}} }{\mathrm{4}{a}}={a} \\ $$$$\mathrm{2}{x}−\mathrm{4}{a}+\mathrm{2}\sqrt{{x}\left({x}−\mathrm{4}{a}\right)}\:=\mathrm{4}{a}^{\mathrm{2}} \\ $$$$\sqrt{{x}\left({x}−\mathrm{4}{a}\right)}\:=\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}−{x} \\ $$$${x}\left({x}−\mathrm{4}{a}\right)=\mathrm{4}{a}^{\mathrm{4}} +\mathrm{4}{a}^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{8}{a}^{\mathrm{3}} −\mathrm{4}{a}^{\mathrm{2}} {x}−\mathrm{4}{ax} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{ax}={x}^{\mathrm{2}} −\mathrm{4}{ax}\left({a}+\mathrm{1}\right)+\mathrm{4}{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}\right) \\ $$$$\mathrm{0}=\mathrm{4}{a}^{\mathrm{2}} \left({a}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {x} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$ \\ $$

Answered by manolex last updated on 01/Jan/23

m=(√x) n=(√(x−4a)) ((m+n)/(m−n))=a m^2 =x n^2 =x−4a m^2 −n^2 =4a (m+n)(m−n)=4a ((m+n)/(m−n))=a m≠n (m+n)^2 =4a^2 m+n=2a ∨ m+n=−2a m−n=2 m−n=−2 2m=2a+2 2m=−2(a+1) m=a+1 m=−(a+1) (√x)=a+1 (√x)=−(a+1) x=(a+1)^2 x=(a+1)^2 solucion x=(a+1)^2 comprobacion ((a+1+(√((a+1)^2 −4a)))/(a+1−(√((a+1)^2 −4a))))=((a+1+(a−1))/(a+1−(a−1)))=((2a)/2)=a correcto

$${m}=\sqrt{{x}} \\ $$$${n}=\sqrt{{x}−\mathrm{4}{a}} \\ $$$$\frac{{m}+{n}}{{m}−{n}}={a} \\ $$$${m}^{\mathrm{2}} ={x} \\ $$$${n}^{\mathrm{2}} ={x}−\mathrm{4}{a} \\ $$$${m}^{\mathrm{2}} −{n}^{\mathrm{2}} =\mathrm{4}{a} \\ $$$$\left({m}+{n}\right)\left({m}−{n}\right)=\mathrm{4}{a} \\ $$$$\frac{{m}+{n}}{{m}−{n}}={a}\:\:\:\:\:\:\:\:{m}\neq{n} \\ $$$$\left({m}+{n}\right)^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \\ $$$${m}+{n}=\mathrm{2}{a}\:\:\:\:\vee\:\:\:\:{m}+{n}=−\mathrm{2}{a} \\ $$$${m}−{n}=\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}−{n}=−\mathrm{2} \\ $$$$\mathrm{2}{m}=\mathrm{2}{a}+\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{2}{m}=−\mathrm{2}\left({a}+\mathrm{1}\right) \\ $$$${m}={a}+\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}=−\left({a}+\mathrm{1}\right) \\ $$$$\sqrt{{x}}={a}+\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{{x}}=−\left({a}+\mathrm{1}\right) \\ $$$${x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${solucion}\:\:\:\:{x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${comprobacion} \\ $$$$\frac{{a}+\mathrm{1}+\sqrt{\left({a}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{a}}}{{a}+\mathrm{1}−\sqrt{\left({a}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{a}}}=\frac{{a}+\mathrm{1}+\left({a}−\mathrm{1}\right)}{{a}+\mathrm{1}−\left({a}−\mathrm{1}\right)}=\frac{\mathrm{2}{a}}{\mathrm{2}}={a}\:\:\:{correcto} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 01/Jan/23

(((√x) + (√(x − 4a)))/( (√x) − (√(x − 4a)))) = a ≠ 0 find “x” in terms of “a”. (√x) +(√(x−4a)) =a(√x) −a(√(x−4a)) a(√x) −(√x) =(√(x−4a)) +a(√(x−4a)) (√x) (a−1)=(√(x−4a)) (a+1) (((√(x−4a)) )/( (√x)))=((a−1)/(a+1)) ((x−4a)/x)=((a^2 −2a+1)/(a^2 +2a+1)) ((x−4a)/x)−1=((a^2 −2a+1)/(a^2 +2a+1))−1 ((−4a)/x)=((−4a)/((a+1)^2 )) (1/x)=(1/((a+1)^2 )) [∵a≠0] x=(a+1)^2

$$\frac{\sqrt{{x}}\:+\:\sqrt{{x}\:−\:\mathrm{4}{a}}}{\:\sqrt{{x}}\:−\:\sqrt{{x}\:−\:\mathrm{4}{a}}}\:=\:{a}\:\neq\:\mathrm{0} \\ $$$$\:{find}\:``{x}''\:{in}\:{terms}\:{of}\:``{a}''.\: \\ $$$$\sqrt{{x}}\:+\sqrt{{x}−\mathrm{4}{a}}\:={a}\sqrt{{x}}\:−{a}\sqrt{{x}−\mathrm{4}{a}}\: \\ $$$${a}\sqrt{{x}}\:−\sqrt{{x}}\:=\sqrt{{x}−\mathrm{4}{a}}\:+{a}\sqrt{{x}−\mathrm{4}{a}} \\ $$$$\sqrt{{x}}\:\left({a}−\mathrm{1}\right)=\sqrt{{x}−\mathrm{4}{a}}\:\left({a}+\mathrm{1}\right) \\ $$$$\frac{\sqrt{{x}−\mathrm{4}{a}}\:}{\:\sqrt{{x}}}=\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\frac{{x}−\mathrm{4}{a}}{{x}}=\frac{{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}} \\ $$$$\frac{{x}−\mathrm{4}{a}}{{x}}−\mathrm{1}=\frac{{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}}−\mathrm{1} \\ $$$$\frac{−\mathrm{4}{a}}{{x}}=\frac{−\mathrm{4}{a}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\:\:\left[\because{a}\neq\mathrm{0}\right] \\ $$$${x}=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com