Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 122461 by benjo_mathlover last updated on 17/Nov/20

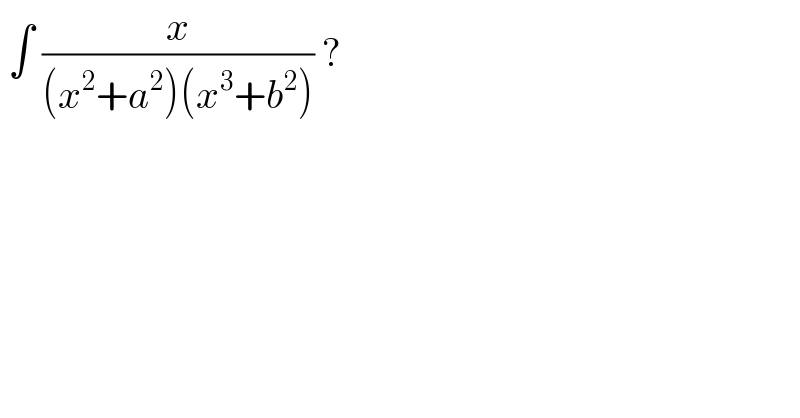
∫ (x/((x^2 +a^2 )(x^3 +b^2 ))) ?

$$\:\int\:\frac{{x}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} +{b}^{\mathrm{2}} \right)}\:? \\ $$

Commented by liberty last updated on 17/Nov/20

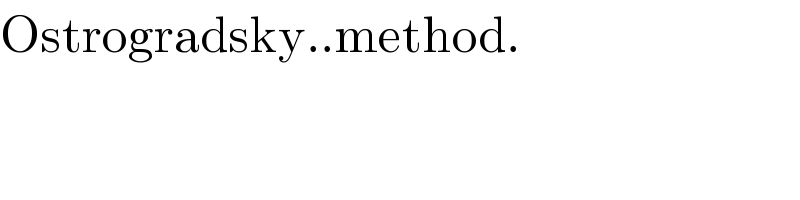
Ostrogradsky..method.

$$\mathrm{Ostrogradsky}..\mathrm{method}.\: \\ $$

Commented by MJS_new last updated on 17/Nov/20

you should search this method on the www to learn when it′s possible to use it. here it′s not possible.

$$\mathrm{you}\:\mathrm{should}\:\mathrm{search}\:\mathrm{this}\:\mathrm{method}\:\mathrm{on}\:\mathrm{the}\:\mathrm{www} \\ $$$$\mathrm{to}\:\mathrm{learn}\:\mathrm{when}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{use}\:\mathrm{it}.\:\mathrm{here}\:\mathrm{it}'\mathrm{s} \\ $$$$\mathrm{not}\:\mathrm{possible}. \\ $$

Answered by MJS_new last updated on 17/Nov/20

this is the solution of ∫(dx/((x^2 +a^2 )(x^3 +b^2 ))) we must decompose... I get I=I_1 +I_2 +I_3 +I_4 +C I_1 =(a^2 /(a^6 +b^4 ))∫(x/(x^2 +a^2 ))dx I_2 =(1/(3(a^2 +b^(4/3) )b^(4/3) ))∫(dx/(x+b^(2/3) )) I_3 =−((a^2 +b^(4/3) )/(6(a^4 −a^2 b^(4/3) +b^(8/3) )b^(4/3) ))∫((2x−b^(2/3) )/(x^2 −b^(2/3) x+b^(4/3) ))dx I_4 =((a^2 −b^(4/3) )/(2(a^4 −a^2 b^(4/3) +b^(8/3) )b^(2/3) ))∫(dx/(x^2 −b^(2/3) x+b^(4/3) )) I_1 =(a^2 /(2(a^6 +b^4 )))ln (x^2 +a^2 ) I_2 =(1/(3(a^2 +b^(4/3) )b^(4/3) ))ln ∣x+b^(2/3) ∣ I_3 =−((a^2 +b^(4/3) )/(6(a^4 −a^2 b^(4/3) +b^(8/3) )b^(4/3) ))ln (x^2 −b^(2/3) x+b^(4/3) ) I_4 =(((a^2 −b^(4/3) )(√3))/(3(a^4 −a^2 b^(4/3) +b^(8/3) )b^(4/3) ))arctan (((2x−b^(2/3) )(√3))/(3b^(2/3) ))

$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} +{b}^{\mathrm{2}} \right)} \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{decompose}...\:\mathrm{I}\:\mathrm{get} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} +{I}_{\mathrm{4}} +{C} \\ $$$${I}_{\mathrm{1}} =\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{6}} +{b}^{\mathrm{4}} }\int\frac{{x}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{4}/\mathrm{3}} \right){b}^{\mathrm{4}/\mathrm{3}} }\int\frac{{dx}}{{x}+{b}^{\mathrm{2}/\mathrm{3}} } \\ $$$${I}_{\mathrm{3}} =−\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{4}/\mathrm{3}} }{\mathrm{6}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{4}/\mathrm{3}} }\int\frac{\mathrm{2}{x}−{b}^{\mathrm{2}/\mathrm{3}} }{{x}^{\mathrm{2}} −{b}^{\mathrm{2}/\mathrm{3}} {x}+{b}^{\mathrm{4}/\mathrm{3}} }{dx} \\ $$$${I}_{\mathrm{4}} =\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{4}/\mathrm{3}} }{\mathrm{2}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{2}/\mathrm{3}} }\int\frac{{dx}}{{x}^{\mathrm{2}} −{b}^{\mathrm{2}/\mathrm{3}} {x}+{b}^{\mathrm{4}/\mathrm{3}} } \\ $$$$ \\ $$$${I}_{\mathrm{1}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left({a}^{\mathrm{6}} +{b}^{\mathrm{4}} \right)}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right) \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{4}/\mathrm{3}} \right){b}^{\mathrm{4}/\mathrm{3}} }\mathrm{ln}\:\mid{x}+{b}^{\mathrm{2}/\mathrm{3}} \mid \\ $$$${I}_{\mathrm{3}} =−\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{4}/\mathrm{3}} }{\mathrm{6}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{4}/\mathrm{3}} }\mathrm{ln}\:\left({x}^{\mathrm{2}} −{b}^{\mathrm{2}/\mathrm{3}} {x}+{b}^{\mathrm{4}/\mathrm{3}} \right) \\ $$$${I}_{\mathrm{4}} =\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{4}/\mathrm{3}} \right)\sqrt{\mathrm{3}}}{\mathrm{3}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{4}/\mathrm{3}} }\mathrm{arctan}\:\frac{\left(\mathrm{2}{x}−{b}^{\mathrm{2}/\mathrm{3}} \right)\sqrt{\mathrm{3}}}{\mathrm{3}{b}^{\mathrm{2}/\mathrm{3}} } \\ $$

Commented by ajfour last updated on 17/Nov/20

oops!

$${oops}! \\ $$

Commented by MJS_new last updated on 17/Nov/20

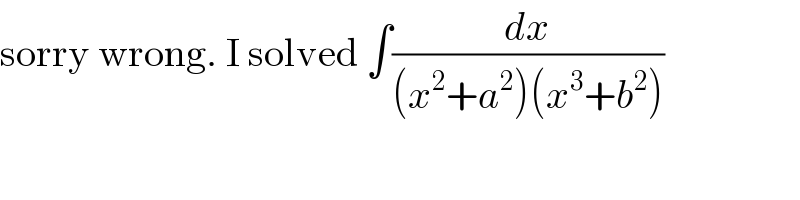
sorry wrong. I solved ∫(dx/((x^2 +a^2 )(x^3 +b^2 )))

$$\mathrm{sorry}\:\mathrm{wrong}.\:\mathrm{I}\:\mathrm{solved}\:\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} +{b}^{\mathrm{2}} \right)} \\ $$

Commented by benjo_mathlover last updated on 17/Nov/20

waw....

$${waw}.... \\ $$

Answered by MJS_new last updated on 17/Nov/20

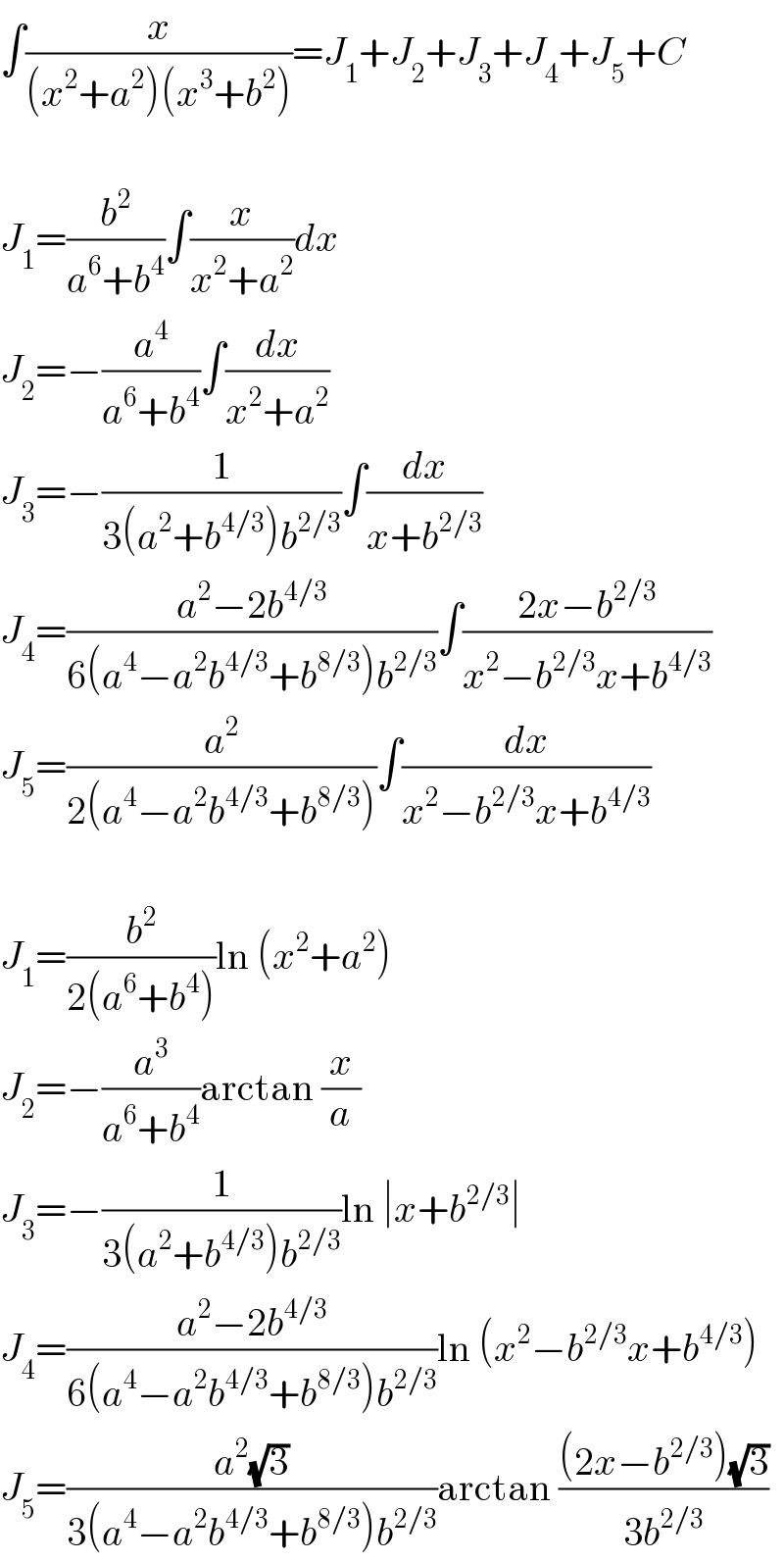
∫(x/((x^2 +a^2 )(x^3 +b^2 )))=J_1 +J_2 +J_3 +J_4 +J_5 +C J_1 =(b^2 /(a^6 +b^4 ))∫(x/(x^2 +a^2 ))dx J_2 =−(a^4 /(a^6 +b^4 ))∫(dx/(x^2 +a^2 )) J_3 =−(1/(3(a^2 +b^(4/3) )b^(2/3) ))∫(dx/(x+b^(2/3) )) J_4 =((a^2 −2b^(4/3) )/(6(a^4 −a^2 b^(4/3) +b^(8/3) )b^(2/3) ))∫((2x−b^(2/3) )/(x^2 −b^(2/3) x+b^(4/3) )) J_5 =(a^2 /(2(a^4 −a^2 b^(4/3) +b^(8/3) )))∫(dx/(x^2 −b^(2/3) x+b^(4/3) )) J_1 =(b^2 /(2(a^6 +b^4 )))ln (x^2 +a^2 ) J_2 =−(a^3 /(a^6 +b^4 ))arctan (x/a) J_3 =−(1/(3(a^2 +b^(4/3) )b^(2/3) ))ln ∣x+b^(2/3) ∣ J_4 =((a^2 −2b^(4/3) )/(6(a^4 −a^2 b^(4/3) +b^(8/3) )b^(2/3) ))ln (x^2 −b^(2/3) x+b^(4/3) ) J_5 =((a^2 (√3))/(3(a^4 −a^2 b^(4/3) +b^(8/3) )b^(2/3) ))arctan (((2x−b^(2/3) )(√3))/(3b^(2/3) ))

$$\int\frac{{x}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\left({x}^{\mathrm{3}} +{b}^{\mathrm{2}} \right)}={J}_{\mathrm{1}} +{J}_{\mathrm{2}} +{J}_{\mathrm{3}} +{J}_{\mathrm{4}} +{J}_{\mathrm{5}} +{C} \\ $$$$ \\ $$$${J}_{\mathrm{1}} =\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{6}} +{b}^{\mathrm{4}} }\int\frac{{x}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx} \\ $$$${J}_{\mathrm{2}} =−\frac{{a}^{\mathrm{4}} }{{a}^{\mathrm{6}} +{b}^{\mathrm{4}} }\int\frac{{dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$$${J}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{4}/\mathrm{3}} \right){b}^{\mathrm{2}/\mathrm{3}} }\int\frac{{dx}}{{x}+{b}^{\mathrm{2}/\mathrm{3}} } \\ $$$${J}_{\mathrm{4}} =\frac{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{4}/\mathrm{3}} }{\mathrm{6}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{2}/\mathrm{3}} }\int\frac{\mathrm{2}{x}−{b}^{\mathrm{2}/\mathrm{3}} }{{x}^{\mathrm{2}} −{b}^{\mathrm{2}/\mathrm{3}} {x}+{b}^{\mathrm{4}/\mathrm{3}} } \\ $$$${J}_{\mathrm{5}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right)}\int\frac{{dx}}{{x}^{\mathrm{2}} −{b}^{\mathrm{2}/\mathrm{3}} {x}+{b}^{\mathrm{4}/\mathrm{3}} } \\ $$$$ \\ $$$${J}_{\mathrm{1}} =\frac{{b}^{\mathrm{2}} }{\mathrm{2}\left({a}^{\mathrm{6}} +{b}^{\mathrm{4}} \right)}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right) \\ $$$${J}_{\mathrm{2}} =−\frac{{a}^{\mathrm{3}} }{{a}^{\mathrm{6}} +{b}^{\mathrm{4}} }\mathrm{arctan}\:\frac{{x}}{{a}} \\ $$$${J}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{4}/\mathrm{3}} \right){b}^{\mathrm{2}/\mathrm{3}} }\mathrm{ln}\:\mid{x}+{b}^{\mathrm{2}/\mathrm{3}} \mid \\ $$$${J}_{\mathrm{4}} =\frac{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{4}/\mathrm{3}} }{\mathrm{6}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{2}/\mathrm{3}} }\mathrm{ln}\:\left({x}^{\mathrm{2}} −{b}^{\mathrm{2}/\mathrm{3}} {x}+{b}^{\mathrm{4}/\mathrm{3}} \right) \\ $$$${J}_{\mathrm{5}} =\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{3}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} {b}^{\mathrm{4}/\mathrm{3}} +{b}^{\mathrm{8}/\mathrm{3}} \right){b}^{\mathrm{2}/\mathrm{3}} }\mathrm{arctan}\:\frac{\left(\mathrm{2}{x}−{b}^{\mathrm{2}/\mathrm{3}} \right)\sqrt{\mathrm{3}}}{\mathrm{3}{b}^{\mathrm{2}/\mathrm{3}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com