
Question Number 105927 by bemath last updated on 01/Aug/20
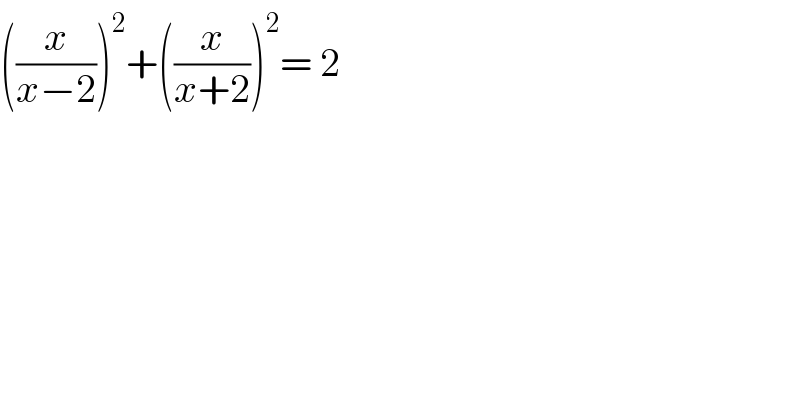
$$\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{2}\: \\ $$
Commented by Rasheed.Sindhi last updated on 02/Aug/20

$$\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{2}\: \\ $$$$\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} =\:\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} \\ $$$${Dividing}\:{by}\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} : \\ $$$$\left(\frac{{x}}{\sqrt{\mathrm{2}}\left({x}−\mathrm{2}\right)}\right)^{\mathrm{2}} +\left(\frac{{x}}{\sqrt{\mathrm{2}}\left({x}+\mathrm{2}\right)}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{{x}^{\mathrm{2}} }{\mathrm{2}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }−\mathrm{1}=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }+\frac{{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{8}{x}−\mathrm{8}}{\mathrm{2}\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} }{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }−\frac{{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$${x}^{\mathrm{2}} \left({x}+\mathrm{2}\right)^{\mathrm{2}} −\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\mathrm{24}{x}^{\mathrm{2}} −\mathrm{32}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{32}}{\mathrm{24}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${x}=\pm\frac{\mathrm{2}}{\sqrt{\mathrm{3}}} \\ $$
Commented by bemath last updated on 02/Aug/20

$${thank}\:{you}\:{both}\: \\ $$
Answered by bobhans last updated on 01/Aug/20

Commented by Rasheed.Sindhi last updated on 02/Aug/20

$$\boldsymbol{{Slightly}}\:\boldsymbol{{different}}{from}\:{above} \\ $$$$\left(\frac{{x}}{{x}−\mathrm{2}}−\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{x}}{{x}−\mathrm{2}}\right)\left(\frac{{x}}{{x}+\mathrm{2}}\right)=\mathrm{2} \\ $$$$\left(\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−{x}^{\mathrm{2}} +\mathrm{2}{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{4}}\right)=\mathrm{2} \\ $$$$\left(\frac{\mathrm{4}{x}}{{x}^{\mathrm{2}} −\mathrm{4}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{4}}\right)=\mathrm{2} \\ $$$$\mathrm{16}{x}^{\mathrm{2}} +\mathrm{2}\left(\frac{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{4}}\right)=\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\mathrm{16}{x}^{\mathrm{2}} +\overset{×} {\mathrm{2}{x}^{\mathrm{4}} }−\mathrm{8}{x}^{\mathrm{2}} =\overset{×} {\mathrm{2}{x}^{\mathrm{4}} }−\mathrm{16}{x}^{\mathrm{2}} +\mathrm{32} \\ $$$$\mathrm{24}{x}^{\mathrm{2}} =\mathrm{32} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{32}}{\mathrm{24}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${x}=\pm\frac{\mathrm{2}}{\sqrt{\mathrm{3}}} \\ $$
Answered by Rasheed.Sindhi last updated on 02/Aug/20
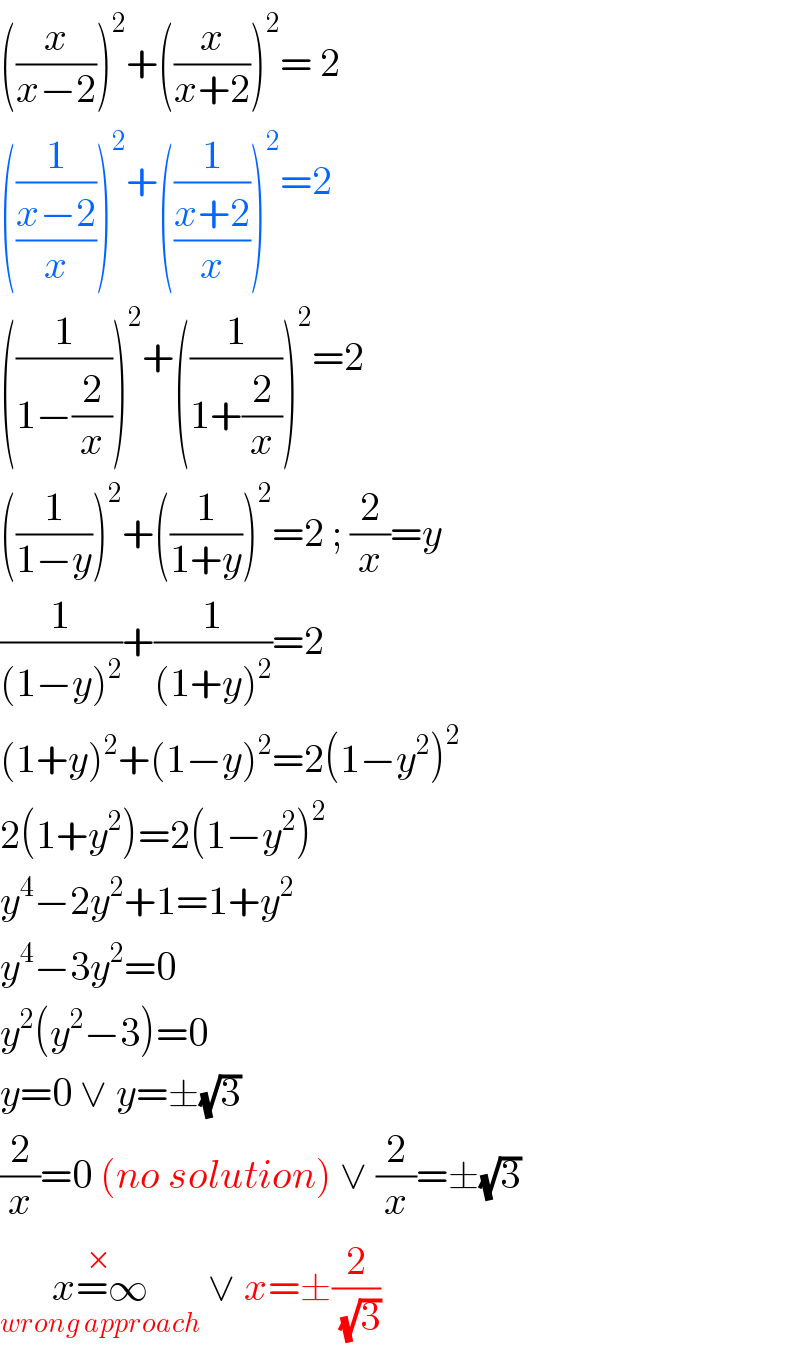
$$\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{2}\: \\ $$$$\left(\frac{\mathrm{1}}{\frac{{x}−\mathrm{2}}{{x}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\frac{{x}+\mathrm{2}}{{x}}}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{2}}{{x}}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}}{{x}}}\right)^{\mathrm{2}} =\mathrm{2}\:\: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{1}−{y}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{1}+{y}}\right)^{\mathrm{2}} =\mathrm{2}\:;\:\frac{\mathrm{2}}{{x}}={y} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{y}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} }=\mathrm{2} \\ $$$$\left(\mathrm{1}+{y}\right)^{\mathrm{2}} +\left(\mathrm{1}−{y}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)=\mathrm{2}\left(\mathrm{1}−{y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{1}+{y}^{\mathrm{2}} \\ $$$${y}^{\mathrm{4}} −\mathrm{3}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$${y}=\mathrm{0}\:\vee\:{y}=\pm\sqrt{\mathrm{3}} \\ $$$$\frac{\mathrm{2}}{{x}}=\mathrm{0}\:\left({no}\:{solution}\right)\:\vee\:\frac{\mathrm{2}}{{x}}=\pm\sqrt{\mathrm{3}} \\ $$$$\underset{{wrong}\:{approach}} {\overset{×} {{x}=\infty}}\:\vee\:{x}=\pm\frac{\mathrm{2}}{\sqrt{\mathrm{3}}} \\ $$
Commented by bobhans last updated on 01/Aug/20
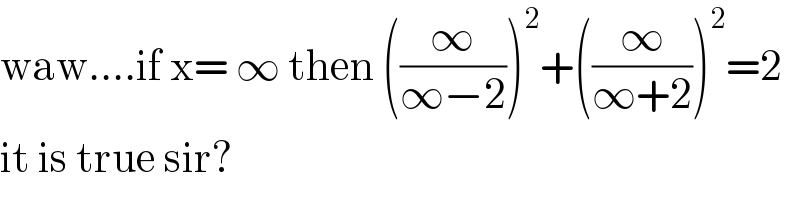
$$\mathrm{waw}....\mathrm{if}\:\mathrm{x}=\:\infty\:\mathrm{then}\:\left(\frac{\infty}{\infty−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\infty}{\infty+\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{sir}?\: \\ $$
Commented by Rasheed.Sindhi last updated on 01/Aug/20

$$\mathcal{S}{ir}\:{I}\:{didn}'{t}\:{try}\:{to}\:{check}\:{the} \\ $$$${equation}\:{back}.\:{Perhaps}\:{this}\:{is} \\ $$$${what}\:{you}\:{have}\:{said}\:``{nothing} \\ $$$${solution}''.{I}\:{think}\:'{nothing} \\ $$$${solution}'\:{is}\:\:{better}. \\ $$$${So}\:,\:\:\:\:\:\frac{\mathrm{2}}{{x}}=\mathrm{0}\Rightarrow\mathrm{2}=\mathrm{0}\left({meaningless}\right) \\ $$$${so}\:{no}\:{solution}. \\ $$$${BTW}\: \\ $$$$\:\:\:\:\frac{\mathrm{2}}{{x}}=\mathrm{0}\:\:\:{and}\:{also}\:\:\:\frac{\mathrm{2}}{\infty}=\mathrm{0} \\ $$$${I}\:{concluded}\:{that}\:{x}=\infty \\ $$
Commented by bobhans last updated on 02/Aug/20
$$\mathrm{ok}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Rasheed.Sindhi last updated on 02/Aug/20
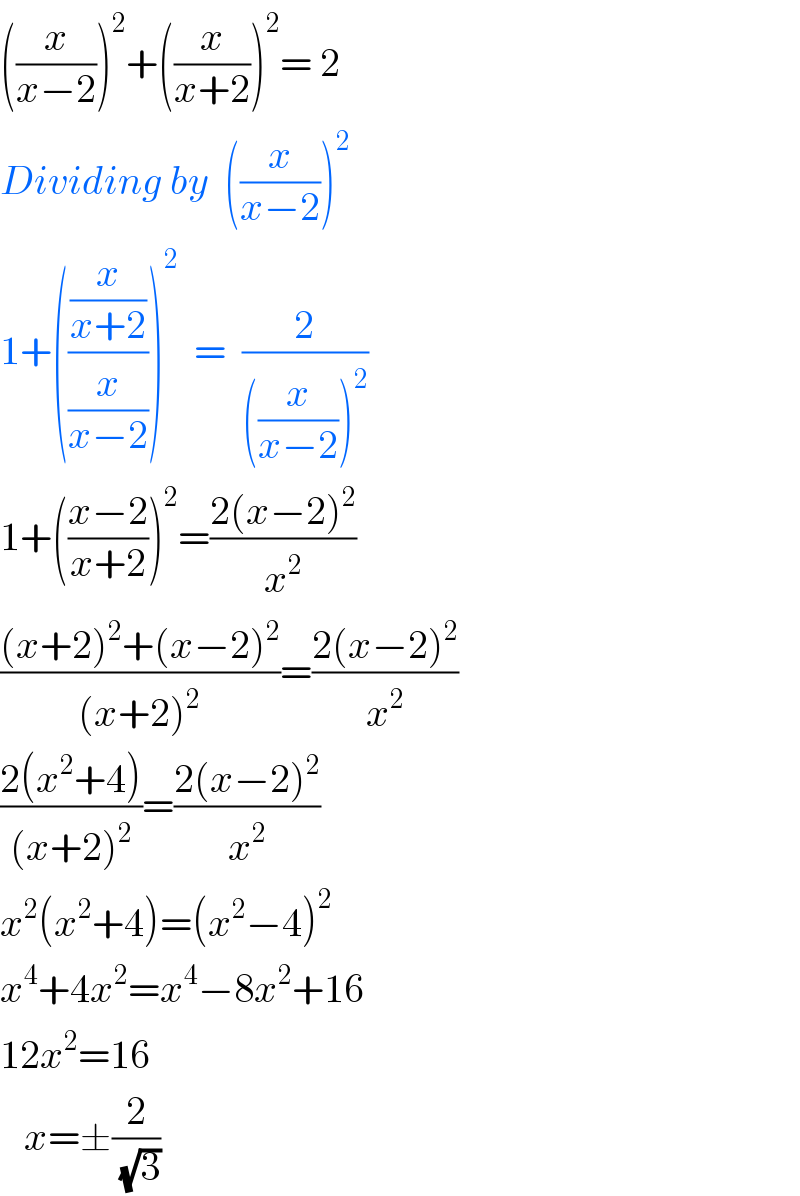
$$\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{2}\: \\ $$$${Dividing}\:{by}\:\:\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}+\left(\frac{\frac{{x}}{{x}+\mathrm{2}}}{\frac{{x}}{{x}−\mathrm{2}}}\right)^{\mathrm{2}} \:\:=\:\:\frac{\mathrm{2}}{\left(\frac{{x}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{1}+\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$\frac{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}\right)=\left({x}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} ={x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{16} \\ $$$$\mathrm{12}{x}^{\mathrm{2}} =\mathrm{16} \\ $$$$\:\:\:{x}=\pm\frac{\mathrm{2}}{\sqrt{\mathrm{3}}} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Aug/20
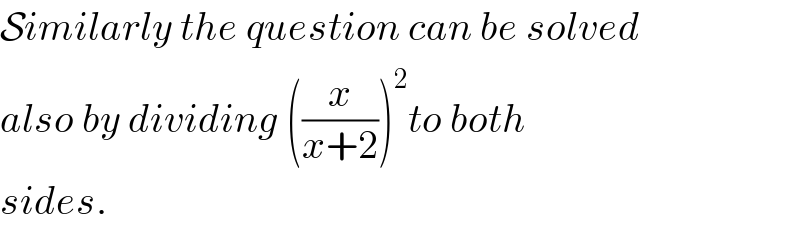
$$\mathcal{S}{imilarly}\:{the}\:{question}\:{can}\:{be}\:{solved} \\ $$$${also}\:{by}\:{dividing}\:\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{\mathrm{2}} {to}\:{both} \\ $$$${sides}. \\ $$
