
Question Number 84809 by M±th+et£s last updated on 16/Mar/20

$$\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {arctan}\left({x}\right)}\:{dx} \\ $$
Commented by abdomathmax last updated on 18/Mar/20
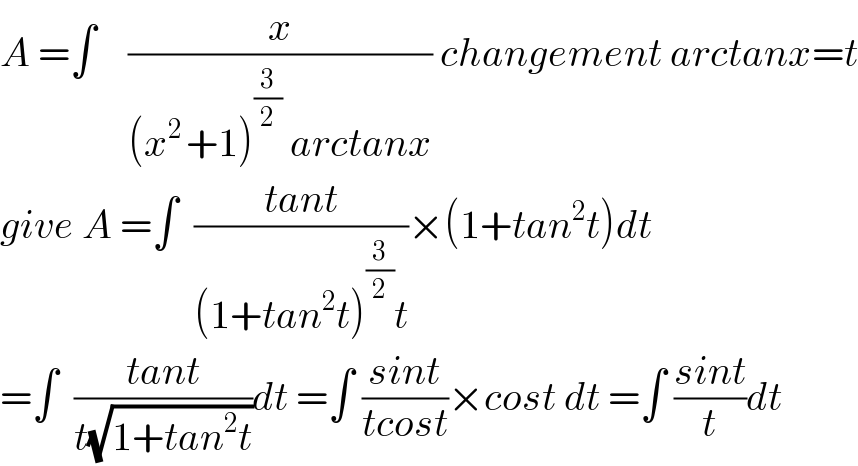
$${A}\:=\int\:\:\:\:\frac{{x}}{\left({x}^{\mathrm{2}\:} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:{arctanx}}\:{changement}\:{arctanx}={t} \\ $$$${give}\:{A}\:=\int\:\:\frac{{tant}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {t}}×\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\int\:\:\frac{{tant}}{{t}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}}{dt}\:=\int\:\frac{{sint}}{{tcost}}×{cost}\:{dt}\:=\int\:\frac{{sint}}{{t}}{dt} \\ $$
Answered by TANMAY PANACEA last updated on 16/Mar/20
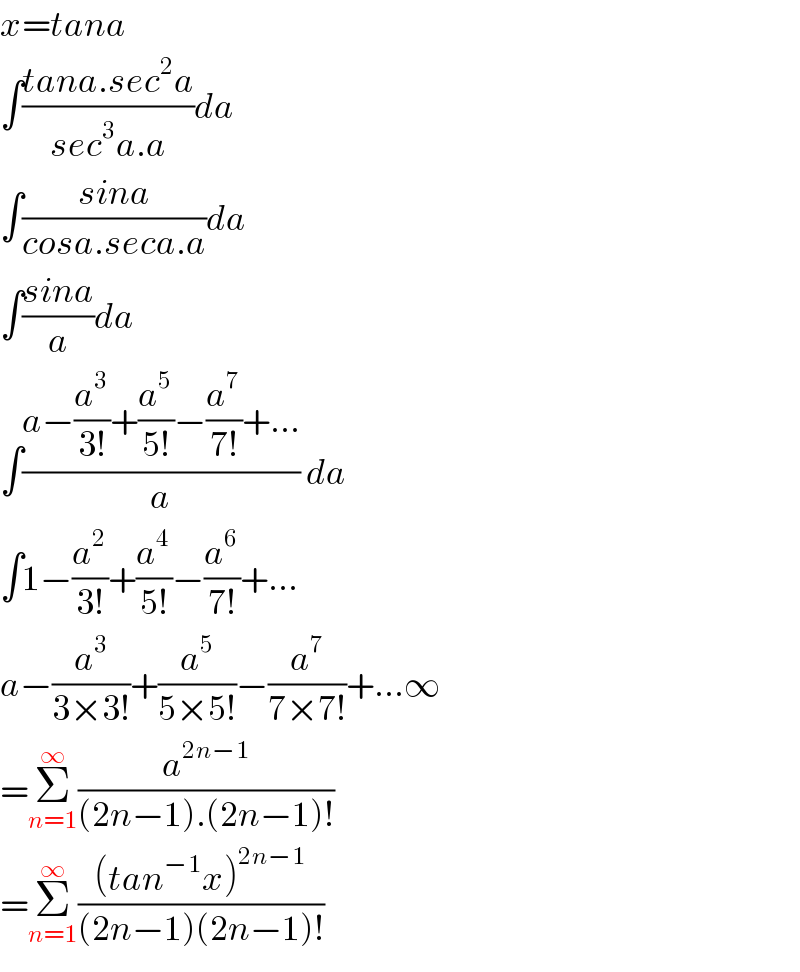
$${x}={tana} \\ $$$$\int\frac{{tana}.{sec}^{\mathrm{2}} {a}}{{sec}^{\mathrm{3}} {a}.{a}}{da} \\ $$$$\int\frac{{sina}}{{cosa}.{seca}.{a}}{da} \\ $$$$\int\frac{{sina}}{{a}}{da} \\ $$$$\int\frac{{a}−\frac{{a}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{a}^{\mathrm{5}} }{\mathrm{5}!}−\frac{{a}^{\mathrm{7}} }{\mathrm{7}!}+...}{{a}}\:{da} \\ $$$$\int\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{a}^{\mathrm{4}} }{\mathrm{5}!}−\frac{{a}^{\mathrm{6}} }{\mathrm{7}!}+... \\ $$$${a}−\frac{{a}^{\mathrm{3}} }{\mathrm{3}×\mathrm{3}!}+\frac{{a}^{\mathrm{5}} }{\mathrm{5}×\mathrm{5}!}−\frac{{a}^{\mathrm{7}} }{\mathrm{7}×\mathrm{7}!}+...\infty \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right).\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({tan}^{−\mathrm{1}} {x}\right)^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$
