
Question Number 6846 by Tawakalitu. last updated on 30/Jul/16
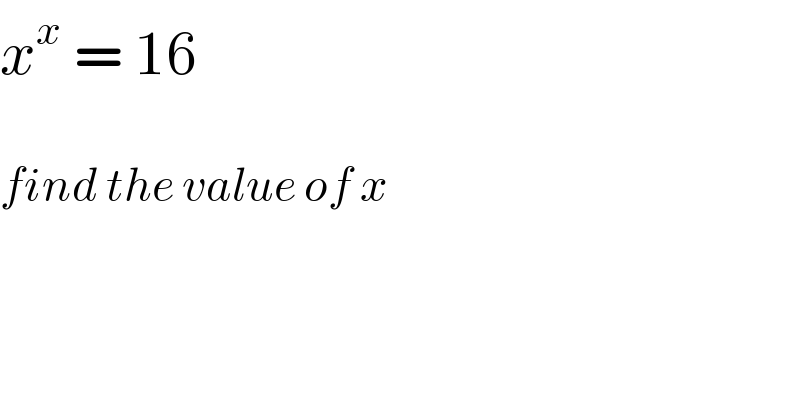
$${x}^{{x}} \:=\:\mathrm{16} \\ $$$$ \\ $$$${find}\:{the}\:{value}\:{of}\:{x}\: \\ $$
Commented by Rasheed Soomro last updated on 31/Jul/16

$$\:\:\mathrm{2}^{\mathrm{2}} <\mathrm{16}<\mathrm{3}^{\mathrm{3}} \\ $$$${So},\:\:\:\:\:\mathrm{2}<{x}<\mathrm{3} \\ $$$${Can}\:{we}\:{determine}\:{x}\:{by}\:\boldsymbol{{interpolation}}? \\ $$$${Question}\:{for}\:{the}\:{sake}\:{of}\:{learning}. \\ $$
Commented by Tawakalitu. last updated on 31/Jul/16
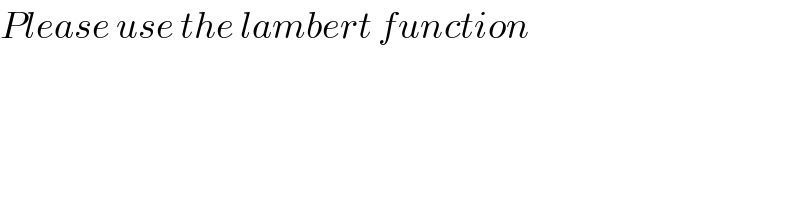
$${Please}\:{use}\:{the}\:{lambert}\:{function} \\ $$
Commented by prakash jain last updated on 31/Jul/16
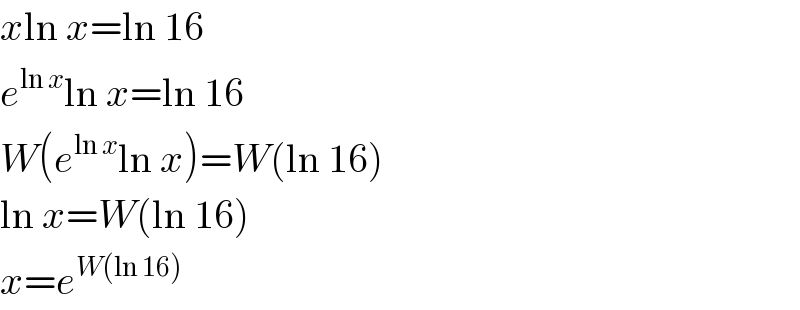
$${x}\mathrm{ln}\:{x}=\mathrm{ln}\:\mathrm{16} \\ $$$${e}^{\mathrm{ln}\:{x}} \mathrm{ln}\:{x}=\mathrm{ln}\:\mathrm{16} \\ $$$${W}\left({e}^{\mathrm{ln}\:{x}} \mathrm{ln}\:{x}\right)={W}\left(\mathrm{ln}\:\mathrm{16}\right) \\ $$$$\mathrm{ln}\:{x}={W}\left(\mathrm{ln}\:\mathrm{16}\right) \\ $$$${x}={e}^{{W}\left(\mathrm{ln}\:\mathrm{16}\right)} \\ $$
Commented by Tawakalitu. last updated on 31/Jul/16

$${Thanks}\:{so}\:{much} \\ $$
