Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 189748 by normans last updated on 21/Mar/23

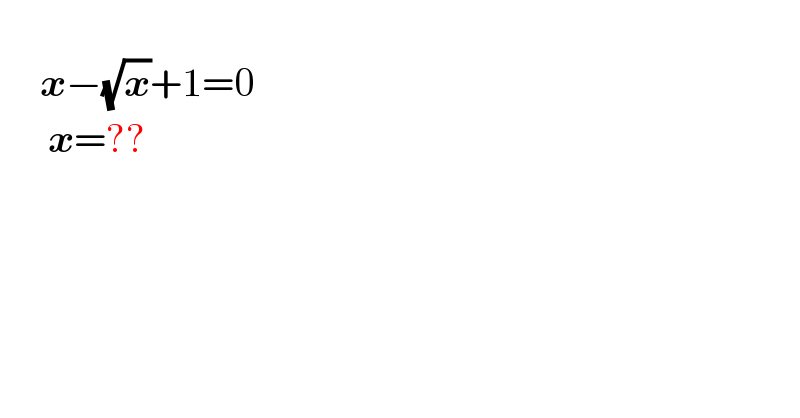
x−(√x)+1=0 x=??

$$ \\ $$$$\:\:\:\:\:\boldsymbol{{x}}−\sqrt{\boldsymbol{{x}}}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\boldsymbol{{x}}=?? \\ $$

Commented by mr W last updated on 21/Mar/23

x>0 (√x)=x+1≥2(√x) 1≥2 ⇒impossible

$${x}>\mathrm{0} \\ $$$$\sqrt{{x}}={x}+\mathrm{1}\geqslant\mathrm{2}\sqrt{{x}} \\ $$$$\mathrm{1}\geqslant\mathrm{2}\:\Rightarrow{impossible} \\ $$

Commented by Frix last updated on 21/Mar/23

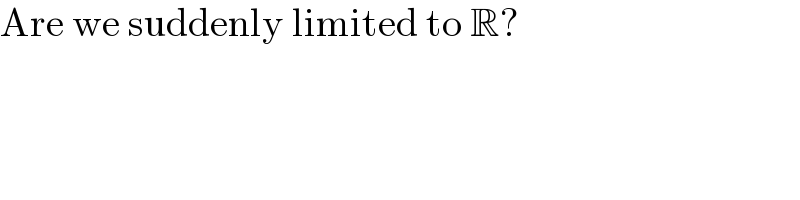
Are we suddenly limited to R?

$$\mathrm{Are}\:\mathrm{we}\:\mathrm{suddenly}\:\mathrm{limited}\:\mathrm{to}\:\mathbb{R}? \\ $$

Answered by TUN last updated on 21/Mar/23

NO ROOT!

$${NO}\:{ROOT}! \\ $$

Answered by Frix last updated on 21/Mar/23

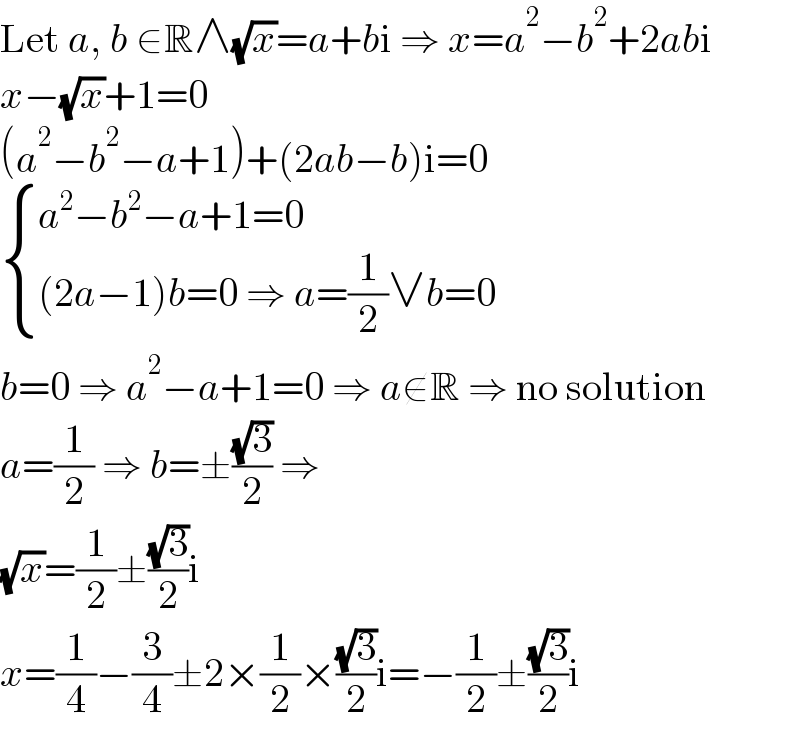
Let a, b ∈R∧(√x)=a+bi ⇒ x=a^2 −b^2 +2abi x−(√x)+1=0 (a^2 −b^2 −a+1)+(2ab−b)i=0 { ((a^2 −b^2 −a+1=0)),(((2a−1)b=0 ⇒ a=(1/2)∨b=0)) :} b=0 ⇒ a^2 −a+1=0 ⇒ a∉R ⇒ no solution a=(1/2) ⇒ b=±((√3)/2) ⇒ (√x)=(1/2)±((√3)/2)i x=(1/4)−(3/4)±2×(1/2)×((√3)/2)i=−(1/2)±((√3)/2)i

$$\mathrm{Let}\:{a},\:{b}\:\in\mathbb{R}\wedge\sqrt{{x}}={a}+{b}\mathrm{i}\:\Rightarrow\:{x}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{ab}\mathrm{i} \\ $$$${x}−\sqrt{{x}}+\mathrm{1}=\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{a}+\mathrm{1}\right)+\left(\mathrm{2}{ab}−{b}\right)\mathrm{i}=\mathrm{0} \\ $$$$\begin{cases}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −{a}+\mathrm{1}=\mathrm{0}}\\{\left(\mathrm{2}{a}−\mathrm{1}\right){b}=\mathrm{0}\:\Rightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\vee{b}=\mathrm{0}}\end{cases} \\ $$$${b}=\mathrm{0}\:\Rightarrow\:{a}^{\mathrm{2}} −{a}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{a}\notin\mathbb{R}\:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{b}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow \\ $$$$\sqrt{{x}}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}\pm\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$

Commented by MJS_new last updated on 21/Mar/23

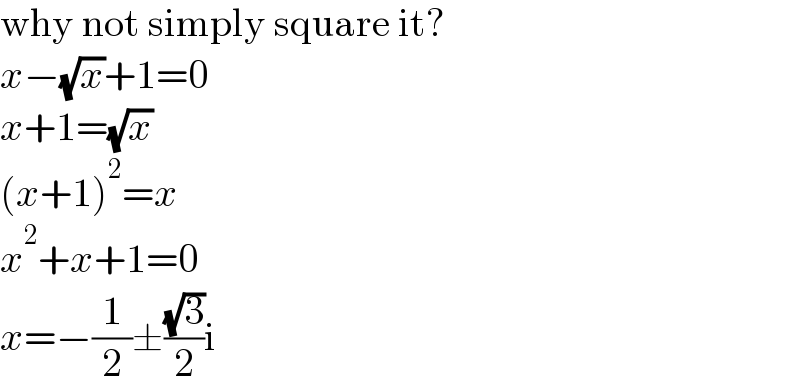
why not simply square it? x−(√x)+1=0 x+1=(√x) (x+1)^2 =x x^2 +x+1=0 x=−(1/2)±((√3)/2)i

$$\mathrm{why}\:\mathrm{not}\:\mathrm{simply}\:\mathrm{square}\:\mathrm{it}? \\ $$$${x}−\sqrt{{x}}+\mathrm{1}=\mathrm{0} \\ $$$${x}+\mathrm{1}=\sqrt{{x}} \\ $$$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} ={x} \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$

Commented by mathocean1 last updated on 21/Mar/23

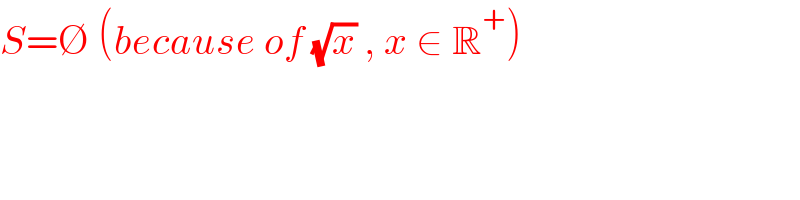
S=∅ (because of (√x) , x ∈ R^+ )

$${S}=\varnothing\:\left({because}\:{of}\:\sqrt{{x}}\:,\:{x}\:\in\:\mathbb{R}^{+} \right) \\ $$$$ \\ $$

Commented by MJS_new last updated on 21/Mar/23

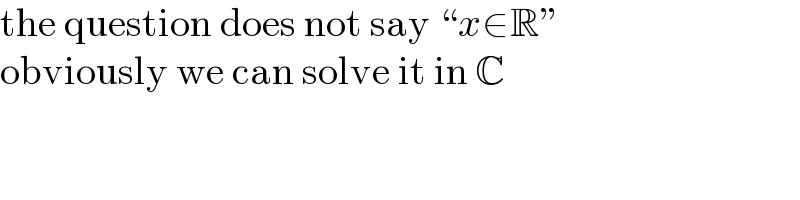
the question does not say “x∈R” obviously we can solve it in C

$$\mathrm{the}\:\mathrm{question}\:\mathrm{does}\:\mathrm{not}\:\mathrm{say}\:``{x}\in\mathbb{R}'' \\ $$$$\mathrm{obviously}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{in}\:\mathbb{C} \\ $$

Commented by talminator2856792 last updated on 22/Mar/23

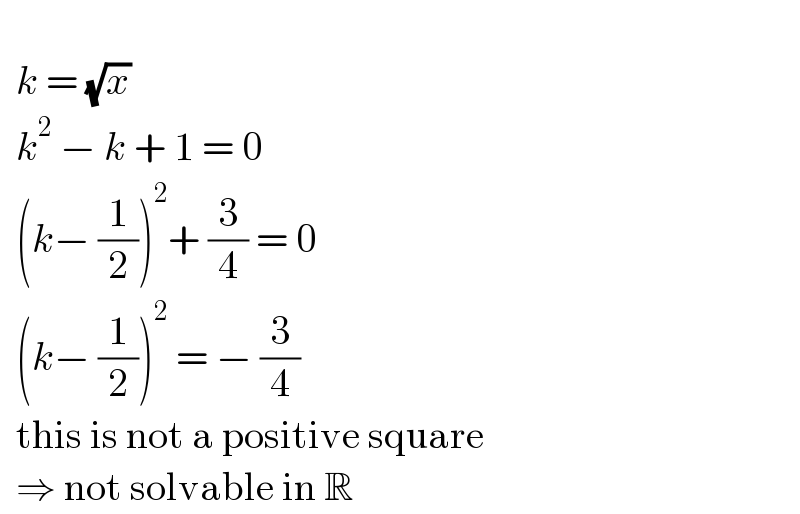
k = (√x) k^2 − k + 1 = 0 (k− (1/2))^2 + (3/4) = 0 (k− (1/2))^2 = − (3/4) this is not a positive square ⇒ not solvable in R

$$ \\ $$$$\:\:{k}\:=\:\sqrt{{x}} \\ $$$$\:\:{k}^{\mathrm{2}} \:−\:{k}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\left({k}−\:\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\:\frac{\mathrm{3}}{\mathrm{4}}\:=\:\mathrm{0} \\ $$$$\:\:\left({k}−\:\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:=\:−\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{square} \\ $$$$\:\:\Rightarrow\:\mathrm{not}\:\mathrm{solvable}\:\mathrm{in}\:\mathbb{R} \\ $$

Commented by MJS_new last updated on 22/Mar/23

yes. but remember Descartes introduced (√(−1))=i back in 1637

$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{remember}\:\mathrm{Descartes}\:\:\mathrm{introduced} \\ $$$$\sqrt{−\mathrm{1}}=\mathrm{i}\:\mathrm{back}\:\mathrm{in}\:\mathrm{1637} \\ $$

Commented by Frix last updated on 22/Mar/23

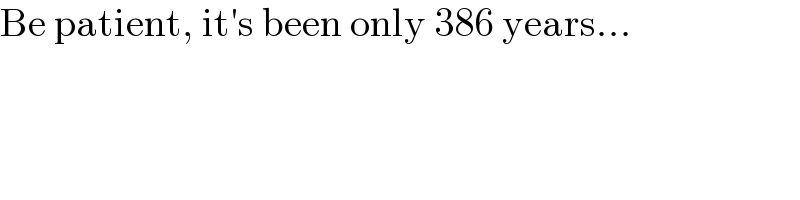
Be patient, it′s been only 386 years...

$$\mathrm{Be}\:\mathrm{patient},\:\mathrm{it}'\mathrm{s}\:\mathrm{been}\:\mathrm{only}\:\mathrm{386}\:\mathrm{years}... \\ $$

Commented by mathocean1 last updated on 27/Mar/23

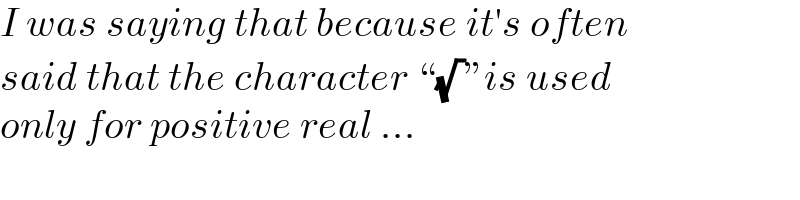
I was saying that because it′s often said that the character “(√ )”is used only for positive real ...

$${I}\:{was}\:{saying}\:{that}\:{because}\:{it}'{s}\:{often} \\ $$$${said}\:{that}\:{the}\:{character}\:``\sqrt{\:}''{is}\:{used} \\ $$$${only}\:{for}\:{positive}\:{real}\:... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com