
Question Number 167335 by Jamshidbek last updated on 13/Mar/22

$$\mathrm{x}_{\mathrm{n}} =\mathrm{n}\centerdot\mathrm{sin}\left(\mathrm{2}\pi\mathrm{en}!\right) \\ $$$$\mathrm{Calculate} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}x}_{\mathrm{n}} \\ $$
Commented by MJS_new last updated on 13/Mar/22
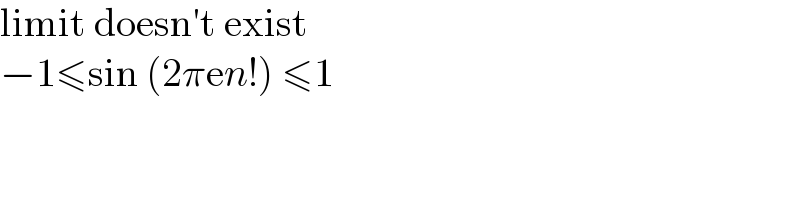
$$\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$$$−\mathrm{1}\leqslant\mathrm{sin}\:\left(\mathrm{2}\pi\mathrm{e}{n}!\right)\:\leqslant\mathrm{1} \\ $$
Commented by Jamshidbek last updated on 13/Mar/22

$$\mathrm{You}\:\mathrm{are}\:\mathrm{wrong}\:\mathrm{thinking} \\ $$
Commented by MJS_new last updated on 13/Mar/22

$$\mathrm{then}\:\mathrm{explain} \\ $$
Answered by abdomsup last updated on 14/Mar/22
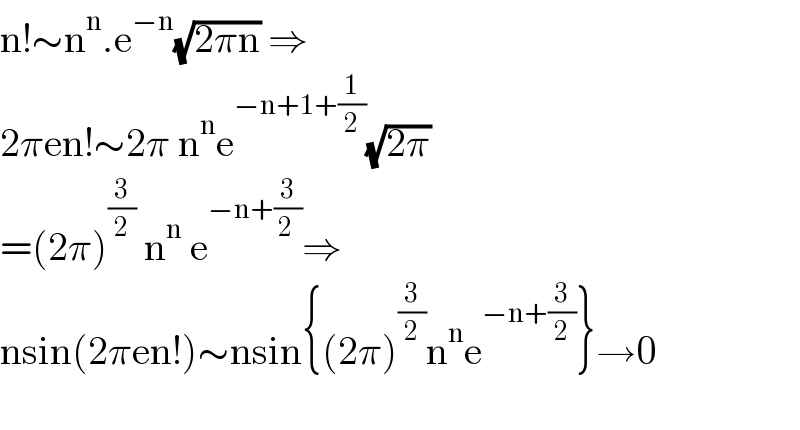
$$\mathrm{n}!\sim\mathrm{n}^{\mathrm{n}} .\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\Rightarrow \\ $$$$\mathrm{2}\pi\mathrm{en}!\sim\mathrm{2}\pi\:\mathrm{n}^{\mathrm{n}} \mathrm{e}^{−\mathrm{n}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{2}\pi} \\ $$$$=\left(\mathrm{2}\pi\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}\:}} \Rightarrow \\ $$$$\mathrm{nsin}\left(\mathrm{2}\pi\mathrm{en}!\right)\sim\mathrm{nsin}\left\{\left(\mathrm{2}\pi\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{n}^{\mathrm{n}} \mathrm{e}^{−\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}} \right\}\rightarrow\mathrm{0} \\ $$$$ \\ $$
Commented by MJS_new last updated on 14/Mar/22
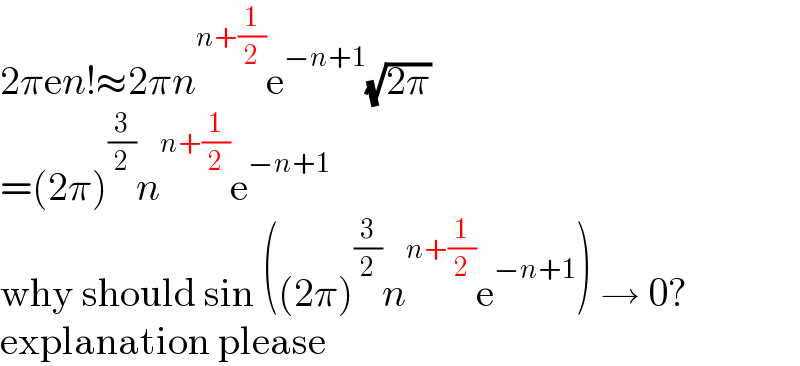
$$\mathrm{2}\pi\mathrm{e}{n}!\approx\mathrm{2}\pi{n}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{e}^{−{n}+\mathrm{1}} \sqrt{\mathrm{2}\pi} \\ $$$$=\left(\mathrm{2}\pi\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {n}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{e}^{−{n}+\mathrm{1}} \\ $$$$\mathrm{why}\:\mathrm{should}\:\mathrm{sin}\:\left(\left(\mathrm{2}\pi\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {n}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{e}^{−{n}+\mathrm{1}} \right)\:\rightarrow\:\mathrm{0}? \\ $$$$\mathrm{explanation}\:\mathrm{please} \\ $$
Commented by Mathspace last updated on 14/Mar/22
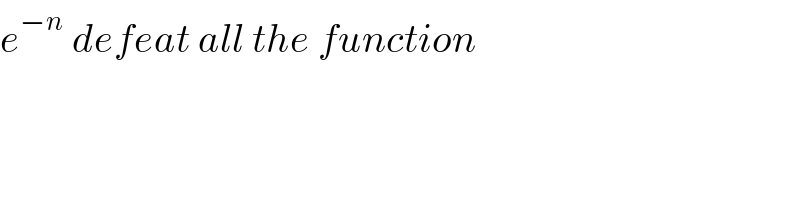
$${e}^{−{n}} \:{defeat}\:{all}\:{the}\:{function} \\ $$
Commented by MJS_new last updated on 14/Mar/22
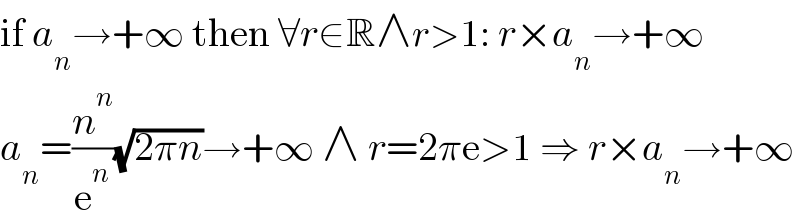
$$\mathrm{if}\:{a}_{{n}} \rightarrow+\infty\:\mathrm{then}\:\forall{r}\in\mathbb{R}\wedge{r}>\mathrm{1}:\:{r}×{a}_{{n}} \rightarrow+\infty \\ $$$${a}_{{n}} =\frac{{n}^{{n}} }{\mathrm{e}^{{n}} }\sqrt{\mathrm{2}\pi{n}}\rightarrow+\infty\:\wedge\:{r}=\mathrm{2}\pi\mathrm{e}>\mathrm{1}\:\Rightarrow\:{r}×{a}_{{n}} \rightarrow+\infty \\ $$
Answered by qaz last updated on 15/Mar/22
![en!=Σ_(k=0) ^n ((n!)/(k!))+Σ_(k=n+1) ^∞ ((n!)/(k!)) =N^+ +(1/(n+1))+(1/((n+1)(n+2)))+... =N^+ +(1/n)(1−(1/n)+(1/n^2 )−...)+(1/n^2 )(1−(1/n)+(1/n^2 )−...)(1−(2/n)+(4/n^2 )−...)+... =N^+ +(1/n)−(1/n^3 )+... ⇒lim_(n→∞) n∙sin (2πen!)=lim_(n→∞) n∙sin [2π(N^+ +(1/n)−(1/n^3 )+...)] =lim_(n→∞) n∙sin [2π((1/n)−(1/n^3 )+...)] =lim_(n→∞) n∙[2π((1/n)−(1/n^3 )+...)−(((2π)^3 )/(3!))∙((1/n)−(1/n^3 )+...)^3 +...] =lim_(n→∞) [2π−((6π+4π^3 )/(3n^2 ))+O((1/n^3 ))] =2π](Q167399.png)
$$\mathrm{en}!=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}!}{\mathrm{k}!}+\underset{\mathrm{k}=\mathrm{n}+\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}!}{\mathrm{k}!} \\ $$$$=\mathbb{N}^{+} +\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}+... \\ $$$$=\mathrm{N}^{+} +\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }−...\right)+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }−...\right)\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{n}}+\frac{\mathrm{4}}{\mathrm{n}^{\mathrm{2}} }−...\right)+... \\ $$$$=\mathrm{N}^{+} +\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }+... \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\centerdot\mathrm{sin}\:\left(\mathrm{2}\pi\mathrm{en}!\right)=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\centerdot\mathrm{sin}\:\left[\mathrm{2}\pi\left(\mathrm{N}^{+} +\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }+...\right)\right] \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\centerdot\mathrm{sin}\:\left[\mathrm{2}\pi\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }+...\right)\right] \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\centerdot\left[\mathrm{2}\pi\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }+...\right)−\frac{\left(\mathrm{2}\pi\right)^{\mathrm{3}} }{\mathrm{3}!}\centerdot\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }+...\right)^{\mathrm{3}} +...\right] \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{2}\pi−\frac{\mathrm{6}\pi+\mathrm{4}\pi^{\mathrm{3}} }{\mathrm{3n}^{\mathrm{2}} }+\mathcal{O}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\right)\right] \\ $$$$=\mathrm{2}\pi \\ $$
Commented by MJS_new last updated on 15/Mar/22
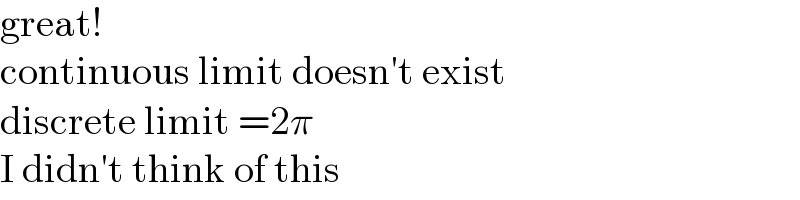
$$\mathrm{great}! \\ $$$$\mathrm{continuous}\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$$$\mathrm{discrete}\:\mathrm{limit}\:=\mathrm{2}\pi \\ $$$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{think}\:\mathrm{of}\:\mathrm{this} \\ $$
