Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 170855 by mnjuly1970 last updated on 01/Jun/22

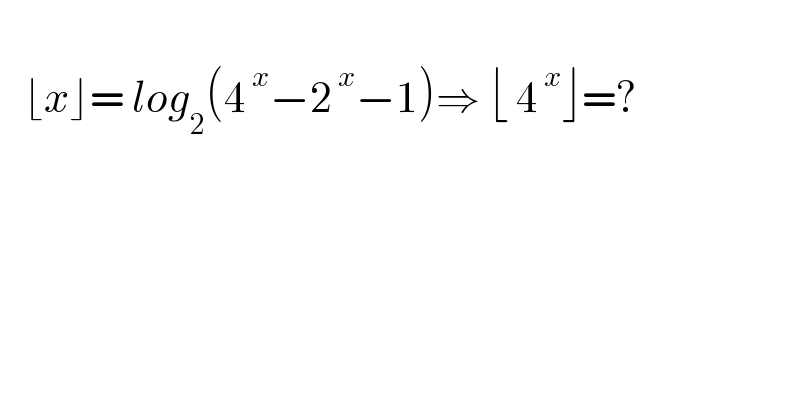
⌊x⌋= log_2 (4^( x) −2^( x) −1)⇒ ⌊ 4^( x) ⌋=?

$$ \\ $$$$\:\:\:\lfloor{x}\rfloor=\:{log}_{\mathrm{2}} \left(\mathrm{4}^{\:{x}} −\mathrm{2}^{\:{x}} −\mathrm{1}\right)\Rightarrow\:\lfloor\:\mathrm{4}^{\:{x}} \rfloor=? \\ $$$$ \\ $$

Answered by floor(10²Eta[1]) last updated on 01/Jun/22

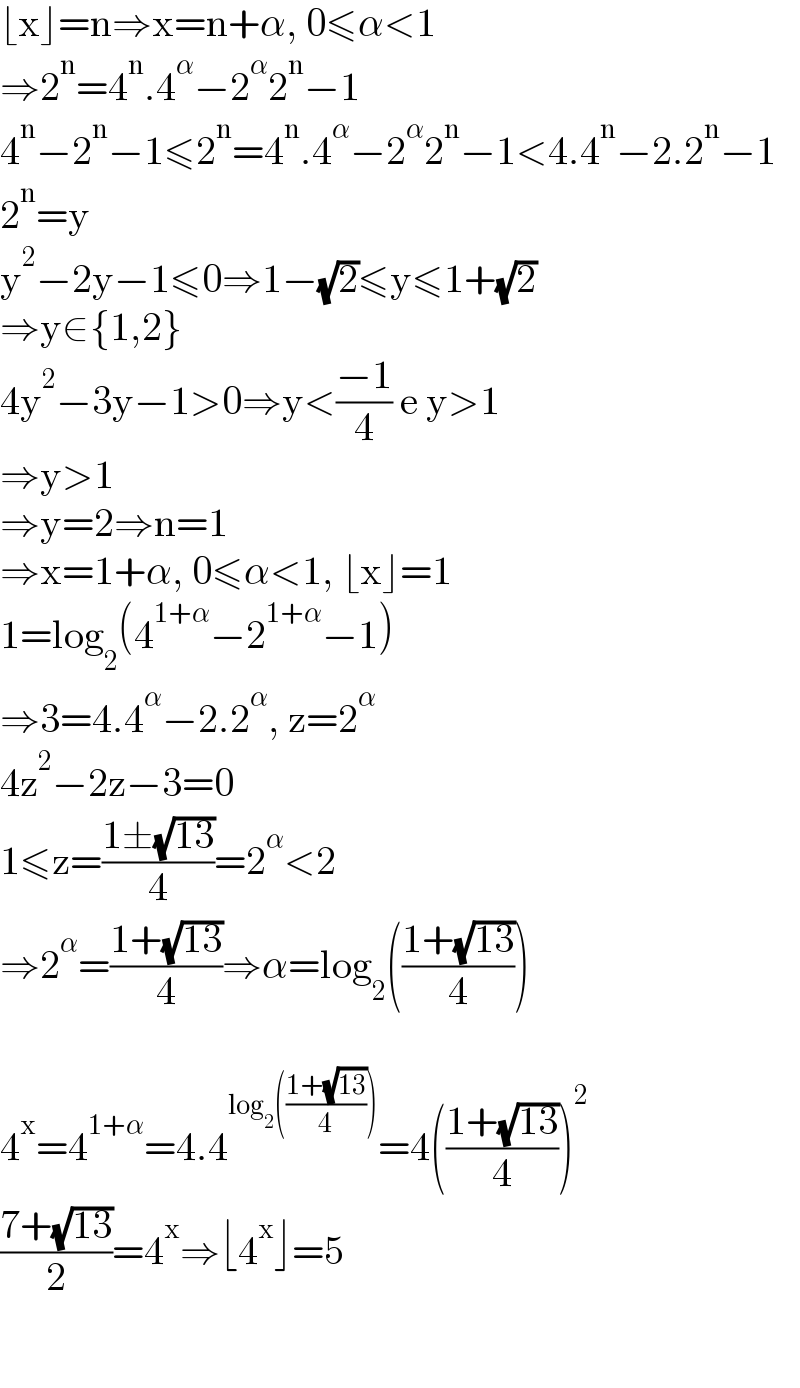
⌊x⌋=n⇒x=n+α, 0≤α<1 ⇒2^n =4^n .4^α −2^α 2^n −1 4^n −2^n −1≤2^n =4^n .4^α −2^α 2^n −1<4.4^n −2.2^n −1 2^n =y y^2 −2y−1≤0⇒1−(√2)≤y≤1+(√2) ⇒y∈{1,2} 4y^2 −3y−1>0⇒y<((−1)/4) e y>1 ⇒y>1 ⇒y=2⇒n=1 ⇒x=1+α, 0≤α<1, ⌊x⌋=1 1=log_2 (4^(1+α) −2^(1+α) −1) ⇒3=4.4^α −2.2^α , z=2^α 4z^2 −2z−3=0 1≤z=((1±(√(13)))/4)=2^α <2 ⇒2^α =((1+(√(13)))/4)⇒α=log_2 (((1+(√(13)))/4)) 4^x =4^(1+α) =4.4^(log_2 (((1+(√(13)))/4))) =4(((1+(√(13)))/4))^2 ((7+(√(13)))/2)=4^x ⇒⌊4^x ⌋=5

$$\lfloor\mathrm{x}\rfloor=\mathrm{n}\Rightarrow\mathrm{x}=\mathrm{n}+\alpha,\:\mathrm{0}\leqslant\alpha<\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{n}} =\mathrm{4}^{\mathrm{n}} .\mathrm{4}^{\alpha} −\mathrm{2}^{\alpha} \mathrm{2}^{\mathrm{n}} −\mathrm{1} \\ $$$$\mathrm{4}^{\mathrm{n}} −\mathrm{2}^{\mathrm{n}} −\mathrm{1}\leqslant\mathrm{2}^{\mathrm{n}} =\mathrm{4}^{\mathrm{n}} .\mathrm{4}^{\alpha} −\mathrm{2}^{\alpha} \mathrm{2}^{\mathrm{n}} −\mathrm{1}<\mathrm{4}.\mathrm{4}^{\mathrm{n}} −\mathrm{2}.\mathrm{2}^{\mathrm{n}} −\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{n}} =\mathrm{y} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\mathrm{1}\leqslant\mathrm{0}\Rightarrow\mathrm{1}−\sqrt{\mathrm{2}}\leqslant\mathrm{y}\leqslant\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}\in\left\{\mathrm{1},\mathrm{2}\right\} \\ $$$$\mathrm{4y}^{\mathrm{2}} −\mathrm{3y}−\mathrm{1}>\mathrm{0}\Rightarrow\mathrm{y}<\frac{−\mathrm{1}}{\mathrm{4}}\:\mathrm{e}\:\mathrm{y}>\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}>\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{2}\Rightarrow\mathrm{n}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{1}+\alpha,\:\mathrm{0}\leqslant\alpha<\mathrm{1},\:\lfloor\mathrm{x}\rfloor=\mathrm{1} \\ $$$$\mathrm{1}=\mathrm{log}_{\mathrm{2}} \left(\mathrm{4}^{\mathrm{1}+\alpha} −\mathrm{2}^{\mathrm{1}+\alpha} −\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{3}=\mathrm{4}.\mathrm{4}^{\alpha} −\mathrm{2}.\mathrm{2}^{\alpha} ,\:\mathrm{z}=\mathrm{2}^{\alpha} \\ $$$$\mathrm{4z}^{\mathrm{2}} −\mathrm{2z}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{1}\leqslant\mathrm{z}=\frac{\mathrm{1}\pm\sqrt{\mathrm{13}}}{\mathrm{4}}=\mathrm{2}^{\alpha} <\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}^{\alpha} =\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{4}}\Rightarrow\alpha=\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$\mathrm{4}^{\mathrm{x}} =\mathrm{4}^{\mathrm{1}+\alpha} =\mathrm{4}.\mathrm{4}^{\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{4}}\right)} =\mathrm{4}\left(\frac{\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{7}+\sqrt{\mathrm{13}}}{\mathrm{2}}=\mathrm{4}^{\mathrm{x}} \Rightarrow\lfloor\mathrm{4}^{\mathrm{x}} \rfloor=\mathrm{5} \\ $$$$ \\ $$

Commented by Tawa11 last updated on 02/Jun/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com