
Question Number 66048 by aliesam last updated on 08/Aug/19
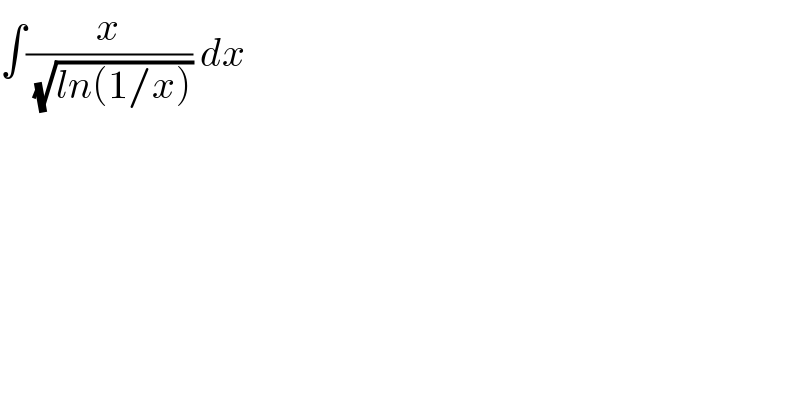
$$\int\frac{{x}}{\sqrt{{ln}\left(\mathrm{1}/{x}\right)}}\:{dx} \\ $$
Commented by Prithwish sen last updated on 08/Aug/19
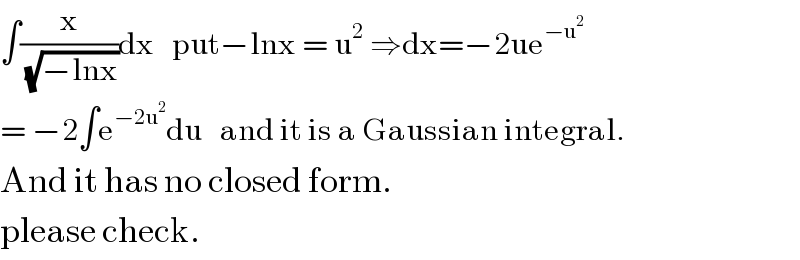
$$\int\frac{\mathrm{x}}{\sqrt{−\mathrm{lnx}}}\mathrm{dx}\:\:\:\mathrm{put}−\mathrm{lnx}\:=\:\mathrm{u}^{\mathrm{2}} \:\Rightarrow\mathrm{dx}=−\mathrm{2ue}^{−\mathrm{u}^{\mathrm{2}} } \\ $$$$=\:−\mathrm{2}\int\mathrm{e}^{−\mathrm{2u}^{\mathrm{2}} } \mathrm{du}\:\:\:\mathrm{and}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{Gaussian}\:\mathrm{integral}. \\ $$$$\mathrm{And}\:\mathrm{it}\:\mathrm{has}\:\mathrm{no}\:\mathrm{closed}\:\mathrm{form}.\: \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
