
Question Number 36595 by rahul 19 last updated on 03/Jun/18
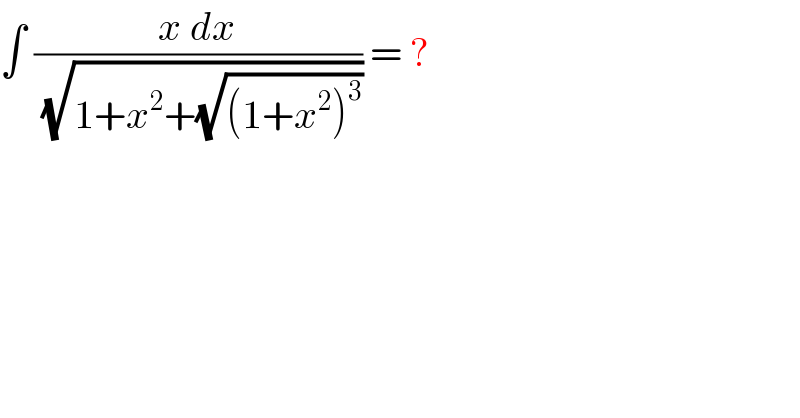
$$\int\:\frac{{x}\:{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} +\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}}\:=\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18
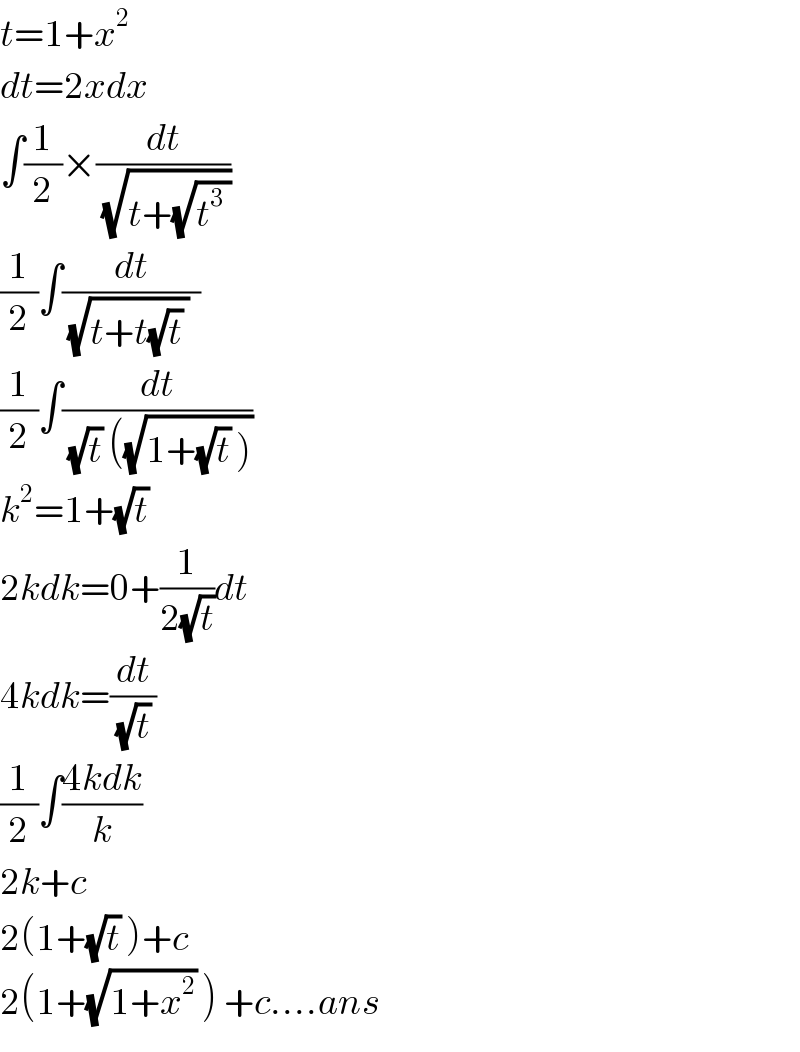
$${t}=\mathrm{1}+{x}^{\mathrm{2}} \\ $$$${dt}=\mathrm{2}{xdx} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{2}}×\frac{{dt}}{\sqrt{{t}+\sqrt{{t}^{\mathrm{3}} \:}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\sqrt{{t}+{t}\sqrt{{t}}\:}\:\:} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\sqrt{{t}}\:\left(\sqrt{\left.\mathrm{1}+\sqrt{{t}}\:\right)}\right.} \\ $$$${k}^{\mathrm{2}} =\mathrm{1}+\sqrt{{t}}\: \\ $$$$\mathrm{2}{kdk}=\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{t}}}{dt} \\ $$$$\mathrm{4}{kdk}=\frac{{dt}}{\sqrt{{t}}\:} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{4}{kdk}}{{k}} \\ $$$$\mathrm{2}{k}+{c} \\ $$$$\mathrm{2}\left(\mathrm{1}+\sqrt{{t}}\:\right)+{c} \\ $$$$\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)\:+{c}....{ans} \\ $$
Commented by rahul 19 last updated on 03/Jun/18
Typo in 2nd last line .
Answered by Joel579 last updated on 03/Jun/18
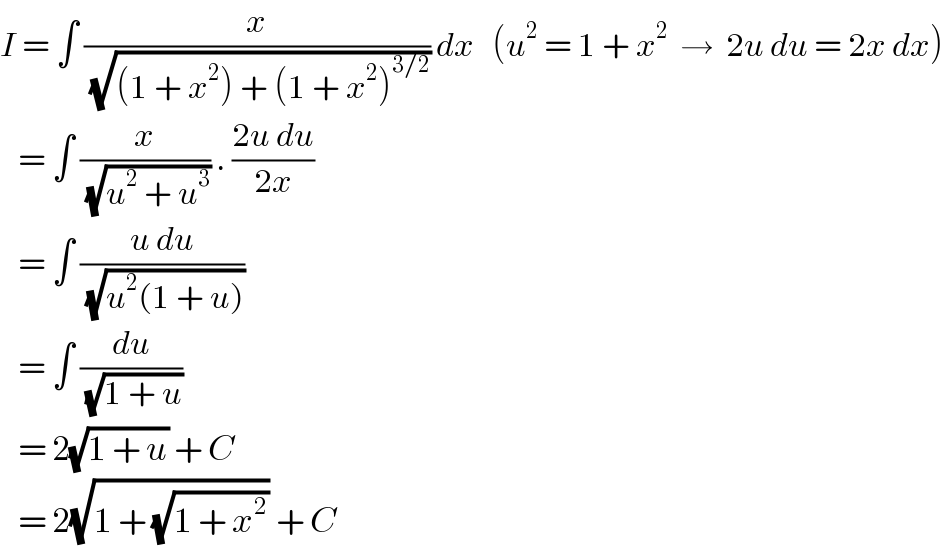
$${I}\:=\:\int\:\frac{{x}}{\sqrt{\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:+\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }}\:{dx}\:\:\:\left({u}^{\mathrm{2}} \:=\:\mathrm{1}\:+\:{x}^{\mathrm{2}} \:\:\rightarrow\:\:\mathrm{2}{u}\:{du}\:=\:\mathrm{2}{x}\:{dx}\right) \\ $$$$\:\:\:=\:\int\:\frac{{x}}{\sqrt{{u}^{\mathrm{2}} \:+\:{u}^{\mathrm{3}} }}\:.\:\frac{\mathrm{2}{u}\:{du}}{\mathrm{2}{x}} \\ $$$$\:\:\:=\:\int\:\frac{{u}\:{du}}{\sqrt{{u}^{\mathrm{2}} \left(\mathrm{1}\:+\:{u}\right)}}\: \\ $$$$\:\:\:=\:\int\:\frac{{du}}{\sqrt{\mathrm{1}\:+\:{u}}} \\ $$$$\:\:\:=\:\mathrm{2}\sqrt{\mathrm{1}\:+\:{u}}\:+\:{C} \\ $$$$\:\:\:=\:\mathrm{2}\sqrt{\mathrm{1}\:+\:\sqrt{\mathrm{1}\:+\:{x}^{\mathrm{2}} }}\:+\:{C} \\ $$
Commented by rahul 19 last updated on 03/Jun/18
thanks sir����
