
Question Number 97417 by MJS last updated on 08/Jun/20
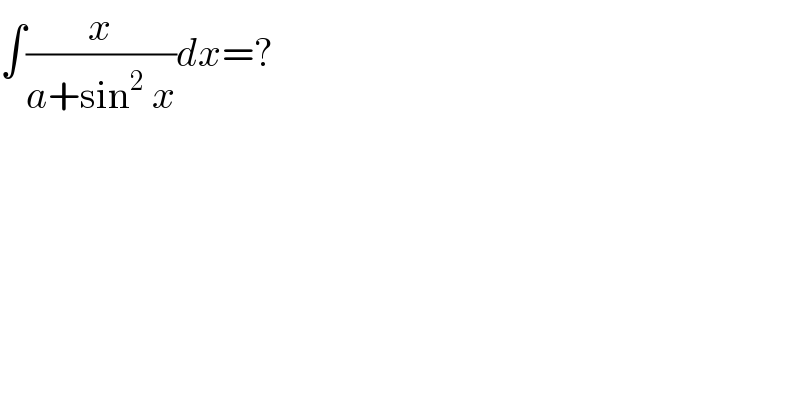
$$\int\frac{{x}}{{a}+\mathrm{sin}^{\mathrm{2}} \:{x}}{dx}=? \\ $$
Answered by MJS last updated on 08/Jun/20
![just found a path: sin x =((e^(ix) −e^(−ix) )/(2i)) ⇒ ∫(x/(a+sin^2 x))dx=4∫((xe^(2ix) )/(4ae^(2ix) −(e^(2ix) −1)^2 ))dx= [t=e^(2ix) −1 → dx=−(i/(2e^(2ix) ))dx] =∫((ln (t+1))/(t^2 −4at−4a))dt now we need to factorize and decompose then substitute to get integrals of the shape ∫((ln (1−u))/u)du=−Li_2 (u) I think it′s only hard to type...](Q97420.png)
$$\mathrm{just}\:\mathrm{found}\:\mathrm{a}\:\mathrm{path}: \\ $$$$\mathrm{sin}\:{x}\:=\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2i}} \\ $$$$\Rightarrow \\ $$$$\int\frac{{x}}{{a}+\mathrm{sin}^{\mathrm{2}} \:{x}}{dx}=\mathrm{4}\int\frac{{x}\mathrm{e}^{\mathrm{2i}{x}} }{\mathrm{4}{a}\mathrm{e}^{\mathrm{2i}{x}} −\left(\mathrm{e}^{\mathrm{2i}{x}} −\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{\mathrm{2i}{x}} −\mathrm{1}\:\rightarrow\:{dx}=−\frac{\mathrm{i}}{\mathrm{2e}^{\mathrm{2i}{x}} }{dx}\right] \\ $$$$=\int\frac{\mathrm{ln}\:\left({t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} −\mathrm{4}{at}−\mathrm{4}{a}}{dt} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{factorize}\:\mathrm{and}\:\mathrm{decompose} \\ $$$$\mathrm{then}\:\mathrm{substitute}\:\mathrm{to}\:\mathrm{get}\:\mathrm{integrals}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shape} \\ $$$$\int\frac{\mathrm{ln}\:\left(\mathrm{1}−{u}\right)}{{u}}{du}=−\mathrm{Li}_{\mathrm{2}} \:\left({u}\right) \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{type}... \\ $$
