
Question Number 167493 by mathlove last updated on 18/Mar/22
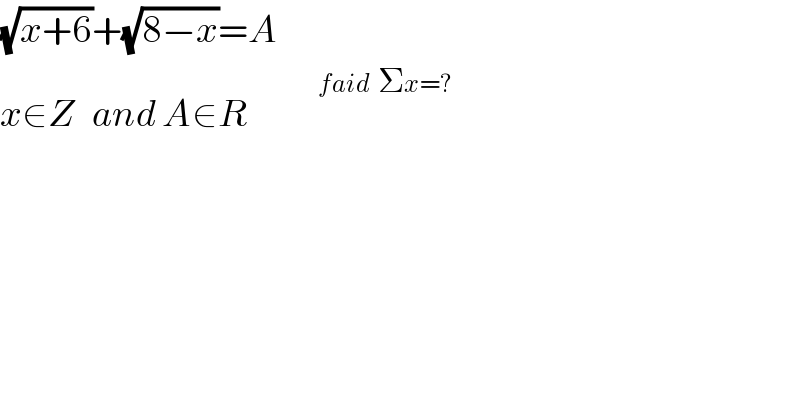
$$\sqrt{{x}+\mathrm{6}}+\sqrt{\mathrm{8}−{x}}={A} \\ $$$${x}\in{Z}\:\:\:{and}\:{A}\in{R}\:\:\:\:\:\:\:\:\:\overset{\:\:\:\:{faid}\:\:\Sigma{x}=?} {\:} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Mar/22
![(√(x+6))+(√(8−x))=A x∈Z and A∈R find Σx. (√(x+6))+(√(8−x))=A∈R ⇒ x+6≥0 ∧ 8−x≥0 [x∈Z] x≥−6 ∧ x≤8 x=−6,−5,−4,...0,1,...,8 Σx=−6−5...−1+0+1...+5+6+7+8=15](Q167495.png)
$$\sqrt{{x}+\mathrm{6}}+\sqrt{\mathrm{8}−{x}}={A} \\ $$$${x}\in{Z}\:\:\:{and}\:{A}\in{R}\:\:\:\:\:\:\:\:\:{find}\:\Sigma{x}. \\ $$$$\sqrt{{x}+\mathrm{6}}+\sqrt{\mathrm{8}−{x}}={A}\in\mathbb{R} \\ $$$$\Rightarrow \\ $$$${x}+\mathrm{6}\geqslant\mathrm{0}\:\wedge\:\mathrm{8}−{x}\geqslant\mathrm{0}\:\:\:\:\left[{x}\in\mathbb{Z}\right] \\ $$$${x}\geqslant−\mathrm{6}\:\wedge\:{x}\leqslant\mathrm{8} \\ $$$${x}=−\mathrm{6},−\mathrm{5},−\mathrm{4},...\mathrm{0},\mathrm{1},...,\mathrm{8} \\ $$$$\Sigma{x}=−\cancel{\mathrm{6}}−\cancel{\mathrm{5}}...−\cancel{\mathrm{1}}+\mathrm{0}+\cancel{\mathrm{1}}...+\cancel{\mathrm{5}}+\cancel{\mathrm{6}}+\mathrm{7}+\mathrm{8}=\mathrm{15} \\ $$
Commented by mathlove last updated on 18/Mar/22

$${thanks}\:{bro} \\ $$
