Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 174092 by behi834171 last updated on 24/Jul/22

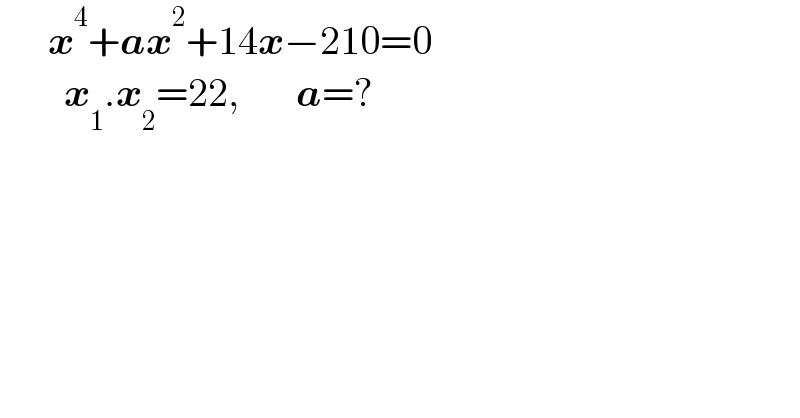
x^4 +ax^2 +14x−210=0 x_1 .x_2 =22, a=?

$$\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{ax}}^{\mathrm{2}} +\mathrm{14}\boldsymbol{{x}}−\mathrm{210}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{{x}}_{\mathrm{1}} .\boldsymbol{{x}}_{\mathrm{2}} =\mathrm{22},\:\:\:\:\:\:\:\boldsymbol{{a}}=? \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jul/22

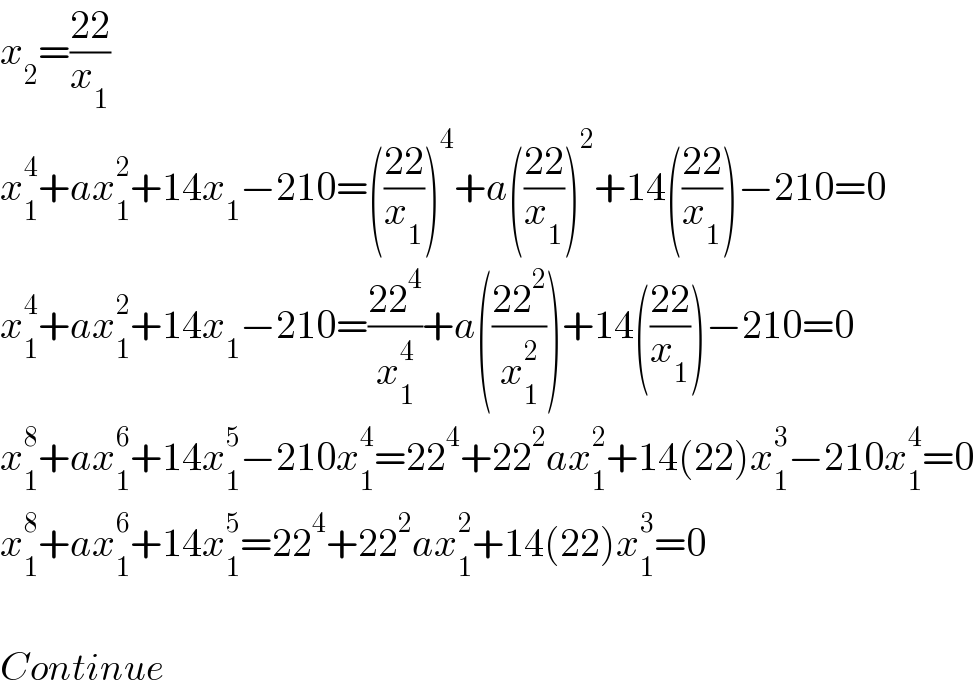
x_2 =((22)/x_1 ) x_1 ^4 +ax_1 ^2 +14x_1 −210=(((22)/x_1 ))^4 +a(((22)/x_1 ))^2 +14(((22)/x_1 ))−210=0 x_1 ^4 +ax_1 ^2 +14x_1 −210=((22^4 )/x_1 ^4 )+a(((22^2 )/x_1 ^2 ))+14(((22)/x_1 ))−210=0 x_1 ^8 +ax_1 ^6 +14x_1 ^5 −210x_1 ^4 =22^4 +22^2 ax_1 ^2 +14(22)x_1 ^3 −210x_1 ^4 =0 x_1 ^8 +ax_1 ^6 +14x_1 ^5 =22^4 +22^2 ax_1 ^2 +14(22)x_1 ^3 =0 Continue

$${x}_{\mathrm{2}} =\frac{\mathrm{22}}{{x}_{\mathrm{1}} } \\ $$$${x}_{\mathrm{1}} ^{\mathrm{4}} +{ax}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{14}{x}_{\mathrm{1}} −\mathrm{210}=\left(\frac{\mathrm{22}}{{x}_{\mathrm{1}} }\right)^{\mathrm{4}} +{a}\left(\frac{\mathrm{22}}{{x}_{\mathrm{1}} }\right)^{\mathrm{2}} +\mathrm{14}\left(\frac{\mathrm{22}}{{x}_{\mathrm{1}} }\right)−\mathrm{210}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{4}} +{ax}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{14}{x}_{\mathrm{1}} −\mathrm{210}=\frac{\mathrm{22}^{\mathrm{4}} }{{x}_{\mathrm{1}} ^{\mathrm{4}} }+{a}\left(\frac{\mathrm{22}^{\mathrm{2}} }{{x}_{\mathrm{1}} ^{\mathrm{2}} }\right)+\mathrm{14}\left(\frac{\mathrm{22}}{{x}_{\mathrm{1}} }\right)−\mathrm{210}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{8}} +{ax}_{\mathrm{1}} ^{\mathrm{6}} +\mathrm{14}{x}_{\mathrm{1}} ^{\mathrm{5}} −\mathrm{210}{x}_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{22}^{\mathrm{4}} +\mathrm{22}^{\mathrm{2}} {ax}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{14}\left(\mathrm{22}\right){x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{210}{x}_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{0} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{8}} +{ax}_{\mathrm{1}} ^{\mathrm{6}} +\mathrm{14}{x}_{\mathrm{1}} ^{\mathrm{5}} =\mathrm{22}^{\mathrm{4}} +\mathrm{22}^{\mathrm{2}} {ax}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{14}\left(\mathrm{22}\right){x}_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{0} \\ $$$$ \\ $$$${Continue} \\ $$

Commented by behi834171 last updated on 24/Jul/22

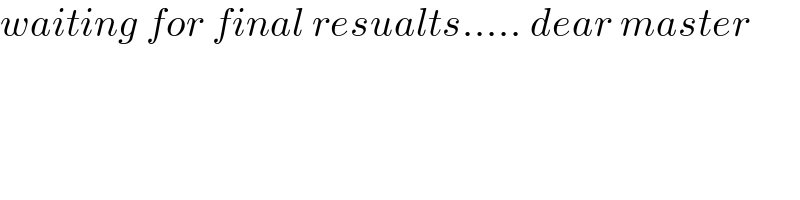
waiting for final resualts..... dear master

$${waiting}\:{for}\:{final}\:{resualts}.....\:{dear}\:{master} \\ $$

Commented by MJS_new last updated on 24/Jul/22

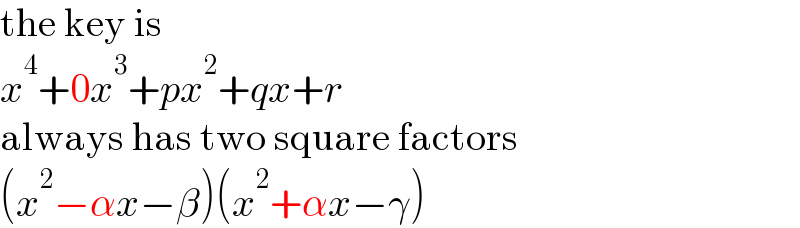
the key is x^4 +0x^3 +px^2 +qx+r always has two square factors (x^2 −αx−β)(x^2 +αx−γ)

$$\mathrm{the}\:\mathrm{key}\:\mathrm{is} \\ $$$${x}^{\mathrm{4}} +\mathrm{0}{x}^{\mathrm{3}} +{px}^{\mathrm{2}} +{qx}+{r} \\ $$$$\mathrm{always}\:\mathrm{has}\:\mathrm{two}\:\mathrm{square}\:\mathrm{factors} \\ $$$$\left({x}^{\mathrm{2}} −\alpha{x}−\beta\right)\left({x}^{\mathrm{2}} +\alpha{x}−\gamma\right) \\ $$

Commented by Rasheed.Sindhi last updated on 25/Jul/22

Thanks for real help sir!

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\mathrm{for}\:\mathrm{real}\:\mathrm{help}\:\boldsymbol{\mathrm{sir}}! \\ $$

Answered by MJS_new last updated on 24/Jul/22

let x_1 =p∧x_2 =((22)/p) ⇒ x^4 +ax^2 +14x−210=(x^2 −((p^2 +22)/p)x+22)(x^2 +((p^2 +22)/p)x−((105)/(11))) since p≠0 we get by matching constants { ((p^2 −((154)/(347))p+22=0)),((a=−((11p^4 +347p^2 +5324)/(11p^2 )))) :} ⇒ p=((77)/(347))±((√(2643069))/(347))i a=((16235157)/(1324499))

$$\mathrm{let}\:{x}_{\mathrm{1}} ={p}\wedge{x}_{\mathrm{2}} =\frac{\mathrm{22}}{{p}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{4}} +{ax}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{210}=\left({x}^{\mathrm{2}} −\frac{{p}^{\mathrm{2}} +\mathrm{22}}{{p}}{x}+\mathrm{22}\right)\left({x}^{\mathrm{2}} +\frac{{p}^{\mathrm{2}} +\mathrm{22}}{{p}}{x}−\frac{\mathrm{105}}{\mathrm{11}}\right) \\ $$$$\mathrm{since}\:{p}\neq\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{by}\:\mathrm{matching}\:\mathrm{constants} \\ $$$$\begin{cases}{{p}^{\mathrm{2}} −\frac{\mathrm{154}}{\mathrm{347}}{p}+\mathrm{22}=\mathrm{0}}\\{{a}=−\frac{\mathrm{11}{p}^{\mathrm{4}} +\mathrm{347}{p}^{\mathrm{2}} +\mathrm{5324}}{\mathrm{11}{p}^{\mathrm{2}} }}\end{cases} \\ $$$$\Rightarrow \\ $$$${p}=\frac{\mathrm{77}}{\mathrm{347}}\pm\frac{\sqrt{\mathrm{2643069}}}{\mathrm{347}}\mathrm{i} \\ $$$${a}=\frac{\mathrm{16235157}}{\mathrm{1324499}} \\ $$

Commented by behi834171 last updated on 24/Jul/22

thank you very much dear master.

$${thank}\:{you}\:{very}\:{much}\:{dear}\:{master}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com