
Question Number 199654 by hardmath last updated on 06/Nov/23
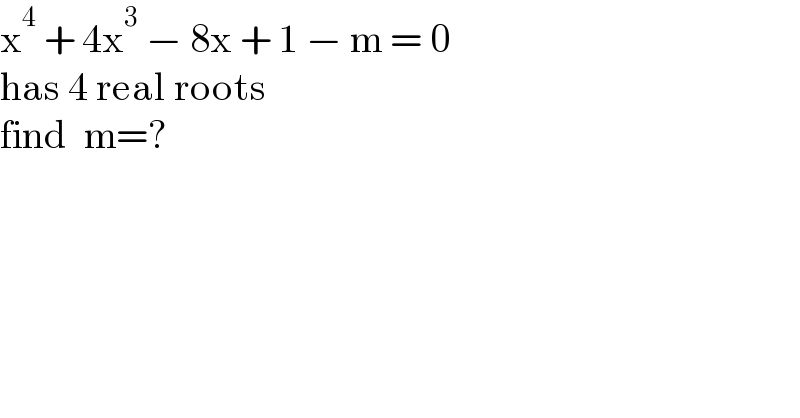
$$\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{4x}^{\mathrm{3}} \:−\:\mathrm{8x}\:+\:\mathrm{1}\:−\:\mathrm{m}\:=\:\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{4}\:\mathrm{real}\:\mathrm{roots} \\ $$$$\mathrm{find}\:\:\mathrm{m}=? \\ $$
Answered by Frix last updated on 07/Nov/23
![This can be factorized and thus solved x=−1±(√(3±(√(m+3)))) [4 combinations of signs] ⇒ m+3>0∧3−(√(m+3))>0 ⇒ −3<m<6](Q199661.png)
$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{factorized}\:\mathrm{and}\:\mathrm{thus}\:\mathrm{solved} \\ $$$${x}=−\mathrm{1}\pm\sqrt{\mathrm{3}\pm\sqrt{{m}+\mathrm{3}}}\:\left[\mathrm{4}\:\mathrm{combinations}\:\mathrm{of}\:\mathrm{signs}\right] \\ $$$$\Rightarrow \\ $$$${m}+\mathrm{3}>\mathrm{0}\wedge\mathrm{3}−\sqrt{{m}+\mathrm{3}}>\mathrm{0} \\ $$$$\Rightarrow \\ $$$$−\mathrm{3}<{m}<\mathrm{6} \\ $$
